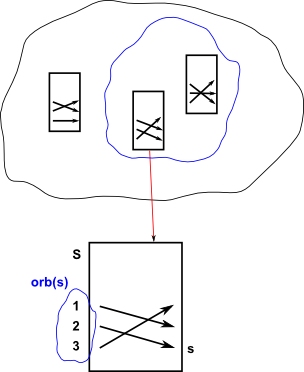
Orbit
orb(s) - When a group G acts on a set S, the orbit of any s in S is the set of elements of S that G arrows can reach from s.
orb(s) = {φ(s) | φ![]() G}
G}
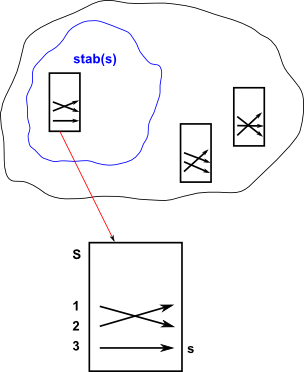
Stabiliser
stab(s) - The stabilizer of an element s in S is the set of group elements g that don't move s. A configuration s in S is called stable if no actions move s.
stab(s) = {φ![]() G | φ(s)=s}
G | φ(s)=s}
Example
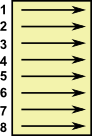
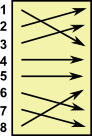
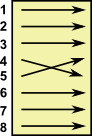
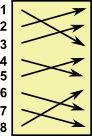
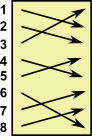
In this example we take 6 permutations named g1 to g6:
g1 |
g2 |
g3 |
 |
 |
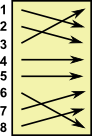 |
g4 |
g5 |
g6 |
 |
 |
 |
we can calculate orb() and stab() examples as follows:
| orb(s) | stab(s) | |orb(s)| · |stab(s)| |
| orb(1)={1,2,3} | stab(1)={g1,g4} | 6 |
| orb(4)={4,5} | stab(4)={g1,g2,g3} | 6 |
| orb(6)={6,7,8} | stab(6)={g1,g4} | 6 |
Orbit-Stabilizer Theorem
The size of an element's orbit times the size of its stabilizer is the size of the group.
|orb(s)| · |stab(s)| = |G|