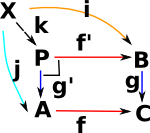So far on these pages we have looked at forms of equality between categories, here we look at how 'equalities' within objects might be represented.
Epimorphism (Surjective) Functions
In category theory we treat objects and functions as black boxes, don't look inside them, but here we will look inside just to get some intuition.
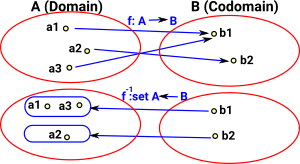
In set theory surjective mappings allow multiple elements in the domain to map to a single element in the codomain. One possible way to interpret this is that all the elements that map to the same element are somehow related - equal in some way or have common properties. Reversing the function gives a fibre bundle. |
 |
More Information
- In set theory terms.
- In category theory terms.
- In type theory terms.
Pullback
The above idea of surjective mappings identifying elements that are somehow equal can be further extended using a pullback.
P is the pullback of f along g or g along f (A,B,C fixed) . Square must commute (in best possible way) so any other square, also containing (A,B,C) must uniquely map to it. |
|
'P' will contain pairs of elements which are somehow 'equal'. That is all possible equations.
More Information
Topoi
More information on this page.