In this category theory section we will use a slightly different notion of a set than we used when we were discussing sets, in their own right, on this page.
One definition of concrete categorories is a set together with some form of 'structure' (by structure we mean functions, mappings and operations within the category). So we can think of sets as being an elemental category without any such structure. Or we could start with some other type of concrete category and apply a 'forgetful functor' to remove the structure.
| So, in this context, we are thinking of a set as a 'bag of points' unrelated to each other in any way. |  |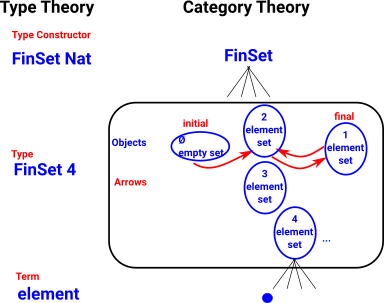
In the diagram above we have a 3 layer hierarchy, at the top we have a node representing all sets. Below that we have various types of sets such as, the empty set, a set with one element, a set with two elements and so on. Below that we have the elements of the sets.
Category theory concentrates on the middle of these 3 layers. That is, we do not derive properties by looking inside at the elements of the sets, instead we derive properties by looking at the mapping between sets.
Special Sets
The Empty Set
This has no elements or points. This is usually denoted 0, Ø or {}.
The One Element (singleton) Set
This has exactly one element (or point). Since category theory tends to compare objects 'up to isomorpism' then, from this point of view, we can't distinguish between one-element-sets so they are effectively the same as each other. This is usually denoted 1.
Set + Structure
In its purest form the only information contained in a set is the number of elements it contains. All other information, such as labeling the elements, can be added using functions between sets.
A total function maps every element in the domain to an element in the codomain. Although not every element in the codomain may necessarily be mapped too. So, in this way functions between sets are not necessarily symmetrical.
From this mathematical structure is genererated.
Bijective functions are invertible. See: |
 |
 |
Surjective functions are not invertible in that we can't reverse the function and get back to where we started, for instance if we have a surjective mapping from set to set we can't get back to the same set, however we can go back to a 'set of sets'. This gives rise to interesting structure, see: |
 |
 |
Injective functions gives a subobject structure. If we have an injective mapping from set to set we can't get back to the same set, however we can have a mapping from set to Bool which tells us which element are in the subset, this is known as a characteristic function in sets or 'subobject classifier' more generally in category theory. This subobject structure is interesting see:
|
 |
 |
This page explains bijection, injection and surjection.
Universal Properties of Set
See this page for a discussion of universal properties.
| Initial | Terminal |
|---|---|
Ø = {} empty set |
{1}or {a} ... one element set |
 |
 |
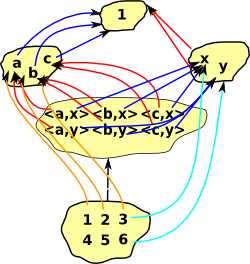
| Product (pullback) |
Sum |
|---|---|
 |
 |
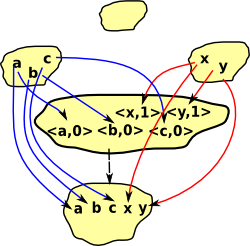cartesian product {a,b,c}*{x,y}= |
disjoint union {a,b,c}+{x,y}= |
Setop
Setop has the same diagrams as set but with the arrows reversed.
So how do we reverse any map between sets? We need something completely equivalent to the reverse not just some unique approximation like adjunctions.
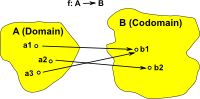
Bijective maps are easy, we just reverse the arrows, but we also want to reverse injective and surjective maps:
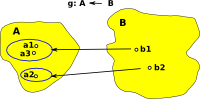
Injective (one-to-one function) In order to reverse an injective function we can reverse all the arrows but we need somewhere for those elements, without arrows, to be mapped back to. A first thought is the empty set. Here we are mapping each element in 'A' to a set (so we have sets within sets), for consistency we also wrap the other elements in their own set. |
  |
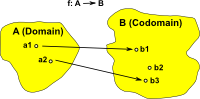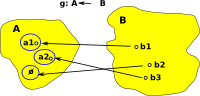Surjective (onto) In order to reverse a surjective function we can again map into a 'set of sets'. This time we replace two arrows from a1 and a3 with a single arrow from a set containing a1 and a3. This single arrow can now be reversed. |
|
So this suggests that the opposite of set could be a set of sets. This complete set of all possible sets of set is known as a powerset.
 |
|
A poweset is sometimes denoted P(Set). Alternative notations are the exponential function: 2set or set -> 2 |
 |
More about Setop on the page here.
