Maths - Setoid Related Categories

On these pages we are looking at set related categories. The category theory of a set is discussed on the page here. We then go on to look at sets with some additional structure. On this page we start to look at sets with an equivalence relation (additional equality structure) added.

Within a set each element must be different, so we can consider equality between elements of different sets or of variables ranging across sets but its not usually useful to consider equality between two elements of the same set. But this is different, here we are adding a new equality over the top of the existing set structure.

First lets look at this structure from a set theoretic point of view. That is we look inside the set, at its elements, rather than looking at its external category theoretic properties. This additional equivalence relation structure partitions the elements of the set into equivalence classes or disjoint (non-overlapping) subsets.

Example Here we have a set labeled as 'A' to 'I' with the following equalities: A~B~C D~E G~H where ~ is the equivalence relation. Sometimes this is denoted with a 3 bar equals sign.

Equivalence Relation

This is a relation between any two elements which has the following properties:

• reflexive: a~a
• transitive: if a~b and b~c then a~c
• symmetric: if a~b then b~a

If S is a set, then an equivalence relation on S can be considered as a subset of S×S or a map S×S-> π where π is the truth object (in this case Boolean).

More about equivalence relation on page here or its category theoretic properties on page here .

So what does the category for this look like?

Quotient Set

One option is to treat the equivalence as if it is the equality so elements that were equivalent now become equal and therefore effectively a single element. Given a set S and an equivalence relation ~ on S, the quotient set of S by ~ is the set S/~ whose elements are the elements of S but where two elements are now considered equal if in S they were merely equivalent. See: ncat.

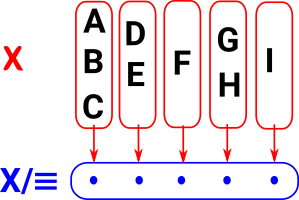Setoid Category

If we want to keep the equivalence separate from the equality then we get a more complicated structure which is a setoid.

Objects
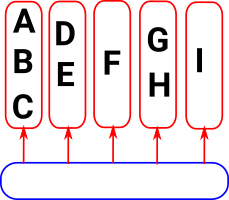Arrows The arrows preserve this additional equality.

Oidification

Oidification allows us to start with a single object and one (or more) arrows back to itself and generalise this to multiple objects. This new structure does not need to have arrows between every pair of objects but composition always exists and every object has an identity arrow.

Here the words 'object' and 'arrow' are used in the category theory sense as described on the page here.

Here are some examples:

	Single Object	Multiple Objects
Setoid This imposes an external equivalence relation and internalises it.	The single object needs to have the reflexive relation, that is, be equal to itself. An example would be a set with a set with a fixed number of elements.	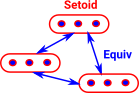Since the arrows are reflexive, symmetric and transitive this gives an equivalence relation.
Groupoid This can be thought of as a weakening of a setiod. Instead of equivalences we have isomorphisms, that is the permutations show how objects are equal in multiple ways.
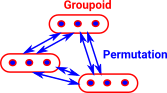Category Just to confuse things the naming conventions have changed here. Monoid has an 'oid' but this is the single object case. A Monoidoid is a category.

See Also

Quotient category wiki

The dual concept to a subobject is a quotient object. wiki

EuclideanSpace

Prerequisites

This page looks at sets from a category theory point of view. For a set theory view see page here.

For an introduction to category theory see page here.

To expand this topic further see Topos Theory.

Books

Sets for Mathematics - This is a book about sets from category theory point of view.