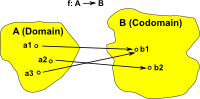
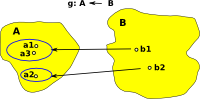
Setop has the same diagrams as set but with the arrows reversed.
So how do we reverse any map between sets? We need something completely equivalent to the reverse not just some unique approximation like adjunctions.
Bijective maps are easy, we just reverse the arrows, but we also want to reverse injective and surjective maps:
Injective (one-to-one function) In order to reverse an injective function we can reverse all the arrows but we need somewhere for those elements, without arrows, to be mapped back to. A first thought is the empty set. Here we are mapping each element in 'A' to a set (so we have sets within sets), for consistency we also wrap the other elements in their own set. |
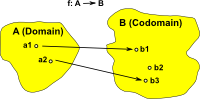 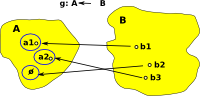 |
Surjective (onto) In order to reverse a surjective function we can again map into a 'set of sets'. This time we replace two arrows from a1 and a3 with a single arrow from a set containing a1 and a3. This single arrow can now be reversed. |
|
So this suggests that the opposite of set could be a set of sets. This complete set of all possible sets of set is known as a powerset.
A poweset is sometimes denoted P(Set). Alternative notations are the exponential function: 2set or set -> 2 |
 |
Functors in Setop
Functor (contravarient) between powersets. In the diagram on the right: element 'a' is mapped to 'a' . Elements 'b' and 'c' are both mapped to 'b'. The diagram shows corresponding powesets. This diagram does not commute but it does send 'x' to a set containing 'x'. |
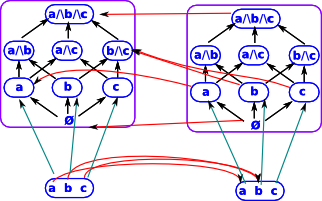 |
Universal Properties in Setop
| Initial | Terminal |
|---|---|
{Ø,set} set containing the empty set and the complete set |
{Ø} set containing the empty set |
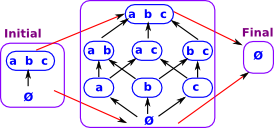 |
|