Setoid
In mathematics, a setoid (X, ~) is a set (or type) X equipped with an equivalence relation ~.
Often in mathematics, when one defines an equivalence relation on a set, one immediately forms the quotient set (turning equivalence into equality). In contrast, setoids may be used when a difference between identity and equivalence must be maintained, often with an interpretation of intensional equality (the equality on the original set) and extensional equality (the equivalence relation, or the equality on the quotient set). - From Wiki
One way to define a setoid is define a tuple consisting of:
- A type T (the carrier set).
- A relation ~.
- A proof that ~ is an equivalence relation over T
- the reflexivity a ~ a.
- the symmetry a ~ b if and only if b ~ a.
- the transitivity if a ~ b and b ~ c, then a ~ c.
Example
So start with some set 'T': This set may already have some structure. |
 |
|
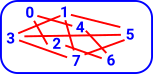 |
We can add extra structure in the form of relations between the elements: | |
| This forms an equivilance relation which divides up the set (in this case into even and odd numbers). | 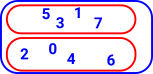 |
|
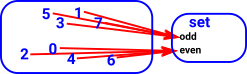 |
Another way to look at this is as a map into set (as a fibre bundle). | |
For an Idris implementation of setoids see this github site
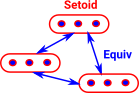
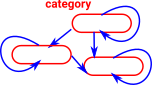
Oidification
Oidification allows us to start with a single object and one (or more) arrows back to itself and generalise this to multiple objects. This new structure does not need to have arrows between every pair of objects but composition always exists and every object has an identity arrow.
Here the words 'object' and 'arrow' are used in the category theory sense as described on the page here.
Here are some examples:
| Single Object | Multiple Objects | |
|---|---|---|
|
This imposes an external equivalence relation and internalises it. |
An example would be a set with a set with a fixed number of elements. |
 Since the arrows are reflexive, symmetric and transitive this gives an equivalence relation. |
|
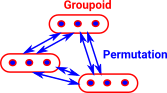
This can be thought of as a weakening of a setiod. Instead of equivalences we have isomorphisms, that is the permutations show how objects are equal in multiple ways. |
 |
|
|
Just to confuse things the naming conventions have changed here. Monoid has an 'oid' but this is the single object case. A Monoidoid is a category. |
 |
 |
Relationship to Groupoid
| Group Definition | Equivalence Definition | |
|---|---|---|
| Identity | a = a•Id = Id •a | reflexivea~a |
| Reverse | a•inv(a) = inv(a)•a = Id | symmetricif a~b then b~a |
| Associatively | a•(b•c) = (a•b)•c | transitiveif a~b and b~c then a~c |
- A setoid is a groupoid without natural coherence axioms.
- A setoid is a groupoid enriched over the cartesian monoidal category of truth values.
- A setoid is a groupoid that is 0-truncated.
Groupoid is explained on this page.
A central idea in the definition of setoid is not to insist upon equality between proof objects.
Extensionality of functions
if f(x) = g(x) for all x
then f = g
Example - consider the two functions f and g mapping from and to natural numbers, defined as follows:
- To find f(x), first add 5 to x, then multiply by 2.
- To find g(x), first multiply x by 2, then add 10.
These functions are extensionally equal; given the same input, both functions always produce the same value. But the definitions of the functions are not equal, and in that intensional sense the functions are not the same.
Functions between Setoids
Extensional Functions between SetoidsA function between setoids is a function between the underlying types (sets) together with a proof of extensionality: A function |f| : |X|->|Y| is extensional, with respect to the equalities of X and Y,if there is a term of type: f ~X=>Y g: Π|x|,|x'|:|X| x ~X x' -> |f|(x) ~Y |f|(y) The bars, as in |x|, indicate x is an element of the underlying type. This distinction will usually be dropped if extensionality applies. |
 |
