Maths - Graph Theory

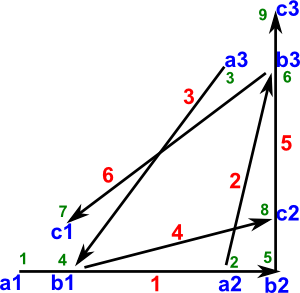
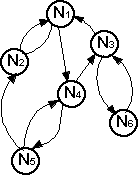
A graph G=(N,U) consists of: A finite set N={n1,n2,...} of nodes. A subset U of the Cartesian product N×N, the elements of which are called arcs. The diagram shows the nodes represented by circles, and arcs (ni,nj) are shown by an arrow drawn from the point representing ni to the point representing nj.

The subset of arcs is shown in the following table.

A more efficient way to encode the graph is as follows:

• A set of named elements (the nodes)
• A set of pairs of names (the arcs)

Where the pairs of names are the names of the start and end nodes.

Types of Graph

There are many variations, a few examples are:

• Undirected graph - the order of the name pairs is not significant.
• Directed graph - the order of the name pairs is significant, the arcs are drawn with an arrow on one end.
• Weighted graph - Nodes or arcs can have a numerical 'weight', for example, to indicate the strength of connection.
• Planar graph - a graph drawn on a plane surface where crossovers only happen at nodes

Relationship to other Mathematical Structures

We can use graphs to represent other mathematical structures. For example Groups can be represented by a 'Cayley graph'. This is a graph, with specific rules, where the arcs have a 'colour' property We could extend this to represent other mathematical structures which have sets+structure.

However graphs, in there most general form, are not necessarily equivalent to an algebraic structure with operations that apply to the whole set (closed operations/functions) in fact graphs can represent partial functions (see also denotational semantics).

Although graphs are not initial algebras it may be possible to use a slightly different structure which is an initial algebra as described on this page.

Graphs are also related to category theory. Category theory diagrams are graphs where:

• The identity arrow, an arc from a node to itself, always exists.
• If adjacent arrows exist then their composition also exists.

For a discussion about using and representing graphs in category theory see this page.

Initial and terminal end-points of an arc.

For an arc (n_i,n_j), the node n_i is the initial end-point and the node n_j is the terminal end-point.

Adjacent nodes

Two nodes are adjacent if they are joined by an arc.

adjacent arcs.

Two arcs are adjacent if they have at least one common end-point.

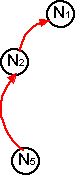
Successors of a node.

A node ni is called a successor of a node x if (ni,nj) U; the set of all successors of x, is denoted by +(ni). In the example, the successors of n1 are (n2,n4), the other successors are:

ni +(ni) n1 (n2,n4) n2 (n1) n3 (n1,n6) n4 (n3,n5) n5 (n2,n4) n6 (n3)

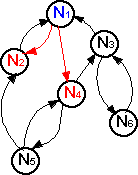
Predecessors of a node.

A node nj is called a predecessor of ni if (nj,ni) U, and the set of all predecessors of n is denoted by -(ni). For example the predecessors of n1 are (n2,n3), the other predecessors are:

ni -(ni) n1 (n2,n3) n2 (n1,n1) n3 (n4,n6) n4 (n1,n5) n5 (n4) n6 (n3)

Arcs incident to and from a node.

If an arc u has node n_i, as its initial end-point, we say that the arc is incident from n_i, whereas if an arc u has node n_i as its terminal end-point we say that arc u is incident to n_i. The number of arcs incident from a node n_i is called the out-degree of n_i and it is denoted by p⁺(n_i); while the number of arcs incident to n_i is called in-degree of x and is denoted by p^-(n_i).

Partial graphs.

If we remove from a graph G (N,U) a subset of its arcs, we are left with a graph of the form:

H = (N,V), where V U

which is called a partial graph of G.

Combining Whole Graphs

So far, we have treated the graph as the whole structure and the nodes and arcs as elements. Here we treat whole graphs as fixed and indivisible and instead apply operations and functions to whole graphs.

Functions Between Graphs

In some cases, perhaps when the graph represents preordered sets, we can define functions between the graphs.

A function between preordered sets is: monotone if x->y implies f(x)->f(y). antitone if x->y implies f(y)->f(x).

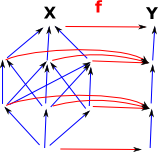More about morpisms between graphs on page here.

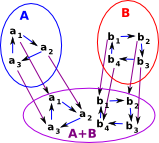
Sum, Product and Exponent of Graphs

There are many operations that we can apply to graphs including:

• Sum - disjoint union
• Product - at least two types of product
  • Cartesian product
  • tensor product
• Exponent - function space.

	Nodes	Arcs
Sum disjoint union	The nodes are added in the same way as sum (disjoint union) of sets.	Arcs are just moved with the corresponding nodes.
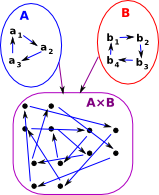
Product Cartesian	We can take the Cartesian product of two domains A and B.	If: a1->a2 and b1->b2 then: <a1,b1>-><a2,b2>
Product tensor		If: a1->a2 and b1->b2 then: <a1,b1>-><a2,b2>
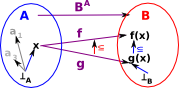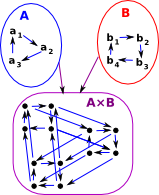
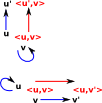
Exponent (function)		For f,gHom(A,B) f->g if f(x)->g(x) for all xA

So to summarise, in both the Cartesian and tensor cases the nodes are the Cartesian product, but the arcs are defined as follows:

Cartesian Product <u,v>-><u',v'> exists: if u=u' and v adj v' or v=v' and u adj u'		AB = AIB + IAB
Tensor Product <u,v>-><u',v'> exists: if u adj u' and v adj v'		AB

Properties

The tensor product is bilinear and associative.

Equivalence Between Graph Products and Kronecker Sum/Product

Cartesian and tensor products not only occur in graphs but also occur in other algebras. In matrix algebra they are known as the Kronecker sum and Kronecker product. This use of the term 'sum' for a product is a bit confusing although it makes some sense in this graphical context since: the nodes are the product nodes but the arcs are in some sense a sum of the component nodes.

For more information see pages about Kronecker sum and Kronecker product.

So an alternative way to calculate a Cartesian or tensor product of two graphs is, to convert the graphs into adjacency matrices(defined below), then take the Kronecker sum or product, then convert back to a graph.

Although the example of an adjacency matrix below has only elements of 0 or 1, if we allow multiple arcs between nodes then, any natural numbers would make sense in this context. It would be hard to interpret adjacency matrix, which had elements that were negative or real numbers, as a graph.

Subgraphs.

If we remove from a graph G = (X,U) a subset nodes, together with all the arcs incident to or from nodes, we are left with a graph of the form:

where:

• M N and Uy=U (M×M)

which is called a subgraph of G. We may describe H, as the subgraph of G generated by Y.

Cliques

A clique is a subset of the nodes of a graph such that there is an edge between every two nodes in the subset.

Cograph

A cograph is a graph all of whose induced subgraphs have the property that any maximal clique intersects any maximal independent set in a single vertex.

Matrix Representations

In addition to outputting to a diagram we can also output other information about the graph in matrix form:

Incidence Matrix

The incidence matrix represents the graph by a matrix of size |V| by |E| see this wiki page
where:

• V=number of vertices
• E=number of edges
• entry [vertex, arrow] = arrow endpoint
• data (simplest case: 1 - incident, 0 - not incident).

Graph	Incidence Matrix
	1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0

Adjacency Matrix

The adjacency matrix is an n by n matrix A, where n is the number of vertices in the graph. If there is an arrow from a vertex x to a vertex y, then the element ax,y is 1 (or in general the number of xy edges), otherwise it is 0. In computing, this matrix makes it easy to find subgraphs, and to reverse a directed graph. see this wiki page

Graph	Adjacency Matrix
	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0

Laplacian Matrix

The laplacian matrix also known as "Kirchhoff matrix" or "Admittance matrix" where:

entry [i,j] =

• inDegree(vi) if i = j (number of incoming links)
• -1 if i not = j and vi is adjacent to vj
• 0 otherwise

Alternatively this is defined as D − A, where D is the diagonal degree matrix. It contains both adjacency information and degree information. There are other, similar matrices, that are also called "Laplacian matrices" of a graph. see this wiki page

Graph	Laplacian Matrix
	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 -1 0 0 0 1 0 0 0 0 0 -1 0 0 0 1 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 -1 0 0 0 1 0 0 0 0 0 -1 0 0 0 1

Distance Matrix

Distance matrices are related to adjacency matrices, with the differences that:

• a) the latter only provides the information which vertices are connected but does not tell about costs or distances between the vertices and
• b) an entry of a distance matrix is smaller if two elements are closer, while "close" (connected) vertices yield larger entries in an adjacency matrix.

see this wiki page

Graph	Distance Matrix
	0 0 0 -1 -1 -1 -1 -1 -1 0 0 0 -1 -1 -1 -1 -1 -1 0 0 0 -1 -1 -1 -1 -1 -1 0 0 1 0 -1 -1 -1 -1 -1 1 0 0 -1 0 -1 -1 -1 -1 0 1 0 -1 -1 0 -1 -1 -1 0 2 0 -1 -1 -1 0 -1 -1 0 0 2 -1 -1 -1 -1 0 -1 2 0 0 -1 -1 -1 -1 -1 0

Other Information about Graph

We now have a graph and we can check out various things about it. We can get information about the whole graph as follows. (10) tells us the graph is acyclic, that is it has no loops (which we can check by looking at the diagram above). (11) tells us that the graph is not functional, that is not every node has a single outgoing arrow. This is what we would expect since an acyclic graph cannot be functional.

(10) -> isAcyclic?(hs3)
   (10)  true
                                                          Type: Boolean
(11) -> isFunctional?(hs3)
   (11)  false
                                                          Type: Boolean

Connected Graphs

If a graph is 'unconnected' then it is not possible to get to parts of the graph from other parts.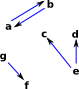
The graph on the right is connected, but only 'weakly connected' because we can only travel between some parts of the graph in one direction.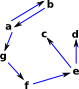
The graph on the right is 'strongly connected' because we can travel between any two nodes in either direction.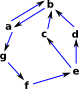
Some graphs are weakly connected but might have islands that are strongly connected.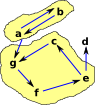

Condensations.

Let P= (n₁,n₂,...,n_J) be a partition of the node-set of a graph G=(X,U). Then the condensation of G induced by P is the graph G_p= (P,U_p) where:

U_p={(X_r,X_s)P×P|X_r ≠ X_s /\ (x_iX_r,x_jX_s | (x_i ,x_j )U)}

In pictorial terms, G_p is obtained from U by coalescing the nodes of each member of P, and then removing any loops.

EuclideanSpace

home

Terminology

A 'graph', in graph theory, is a set of nodes and a set of lines between them. Note that this is a different meaning of the word 'graph' from the other way that it is used in mathematics as a graphical representation of the relationship between continuously varying quantities.

There is a sense where these two meanings of the word 'graph' can be dual to each other. We will describe this later.

Prerequisites

For a category theory perspective then see a page about monoidal categories here. This page illustrates some issues from monoidal categories using graphs as an example.

Computing Graphs

There is a program which can represent and do calculations on graph theory on this page.

Problem Solving

Data Types

Functional Programming and Category Theory