SingletonIn 'set', a singleton is a set with one element (its cardinality is 1). A singleton has the property that every function from it to any arbitrary set is injective. This concept is not limited to sets, for example, singleton list or 1-tuple. |
In computing, there is the unit type. See page here.
In category theory we need to express this concept externally (without looking inside it to see how many elements it has).
Contractibility of SingletonsThis is saying that there is an element 'x' that is equal to every other element of the set. This implies that there is only one element of the set. So how can 'a' potentially represent multiple elements. Perhaps we can work with multiple types of equality and this equality is being imposed externally. So whether a given set is a singleton might depend on the equality used. |
| This code represents a singleton, it is saying: for a type 'A' and any element of that type 'a' there exists a unique path to a point 'x'. |
singl (A : U) (a : A) : U
= (x : A) * Path A a x
CubicalTT code from here. |
This seems quite trivial for conventional set theory. However in HoTT things can get more interesting and this becomes an important concept.
Contractible Type
https://homotopytypetheory.org/2017/09/16/a-hands-on-introduction-to-cubicaltt/
Contractibility of Singletons
The following uses notation and ideas from cubical type theory on the page here.
This proves the singleton defined in the code above is contractible. For a type 'A' and any two elements 'a' and 'b' and a path between those points 'p'. |
contrSingl (A : U) (a b : A) (p : Path A a b) :
Path (singl A a) (a,<i> a) (b,p) =
<i> (p @ i,<j> p @ i /\ j)
CubicalTT code from here. |
| This proof produces a path between two singletons like this: | 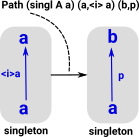 |
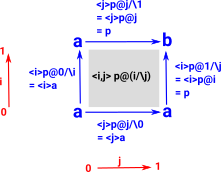 |
This path is a type and to prove it we must construct an instance of the type. The first component of the above pair has to be a path from a to b, this is what p @ i gives us (note that we are to the right of <i> so that i is now in context). The second component should be a square connecting <i> a to p and this is what the square for p @ i /\ j in this diagram gives us. |