Maths - Empty and Unit Types

Here are some more atomic types, this time denoted in a more category theory way:

Type Term  
0 ⊥ empty type (initial)
1 ⊤ unit type (terminal)
2 True
False		 boolean

Empty Type

ref

Denoted 'empty' or 0 or bottom or _|_ .

We cannot introduce a term. If we do have a term then we can prove any other type. So we have no arrows in but we have arrows going out to every other type. 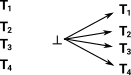bottom

as a negative type:

Notation

Rules

Types are defined by their formation, term introduction, term eliminator and computation rules:

 

Empty Type

formation rule

It exists

 
Ø:Type

term introduction rule

 There is no introduction rule
term eliminator
Γright adjointp:Ø   Γright adjointC:Type
Γright adjointabort(p):C
computation rule There is no computation rule

Local completeness rule

  

Implemetations of Empty

Idris

from : Idris-dev/libs/prelude/Builtins.idr

 
||| The empty type, also known as the trivially false proposition.
|||
||| Use `void` or `absurd` to prove anything if
||| you have a variable of type `Void` in scope.
data Void : Type where

||| The eliminator for the `Void` type.
void : Void -> a

COQ

from : coq/theories/Init/Datatypes.v 

(** [Empty_set] is a datatype with no inhabitant *)

Inductive Empty_set : Set :=.

Unit Type

ref1 ref2

Denoted 'unit' or 1 or top or T .

Unit is related to the idea of a singleton type (see page here)

Unit is always true, we can introduce a term without any additional information.

There is a sense that this is the inverse of the empty type:

  • empty type can not be introduced
  • unit type can always by introduced
top

The term of the unit type is thought of as the null tuple (). This is because of the way that it works with the product type:

(x,()) =β (x)

In computing this equality does not hold exactly, however it is true upto isomorphism (or upto beta equality), that is, both sides of the equation contain the same information.

Can we use unit type to build enumeration types? Example 2=1+1. That would be more like a tuple with one element? unit(C)? which does not seem to be what we have here?

In the propositions-as-types approach the unit type corresponds to 'mere' propositions are the propositions in classical logic. This allows us to use the law of excluded middle when appropriate (for set-like structures).

The 'unit' type, in homotopy collapses to a point so, in that way, it is the most fundamental type.

 

Unit Type

formation rule

Unit type exists and does not depend on anything.

 
right adjointunit :Type

term introduction rule

Unit is always true, we can introduce a term without any additional information.
 
right adjointtt :unit

term eliminator

p:unit /\ c = c

If we know how to produce a C using all the possible inputs that can go into a unit, then we can produce a C from any unit.

Γright adjoint():unit   Γright adjointC:Type   Γright adjointc:C
Γright adjointtriv((),c):C

computation rule

When we evaluate the eliminator on a term of canonical form, we obtain the data that went into the eliminator associated with that form

Γright adjointC:Type   Γright adjointc:C
Γright adjointtriv((),c)->β c

Local completeness rule

  

Implemetations of Unit

Idris

from : Idris-dev/libs/prelude/Builtins.idr

 
||| The canonical single-element type, also known as the trivially
||| true proposition.
data Unit =
  ||| The trivial constructor for `()`.
  MkUnit

COQ

from : coq/theories/Init/Datatypes.v 

(** [unit] is a singleton datatype with sole inhabitant [tt] *)

Inductive unit : Set :=
tt : unit.

2 (bool)

A set with two elements. This is the data type of Boolean algebra). It is like sum (either) where the terms are not necessarily types.

 

Unit Type

formation rule

Unit type exists and does not depend on anything.

 
right adjoint2 :Type

term introduction rule

Lets call the two elements 'true' and 'false' as tends to be used in Boolean algebra. There is one constructor for each of these.
     
right adjointfalse :2   right adjointtrue :2

term eliminator

Like sum (either) the deconstructor requires a type 'C' and map a map from each of the elements to C. In practice we can implement this as a case-statement or even an if-then-else.
x:2right adjointC(x):Type   right adjointfalse:C(0)   Γright adjointtrue:C(1)
x:2right adjoint2rec(x,false,true):C(x)

computation rule

There are 2 equalities, one for 'false' and one for 'true'

x:2right adjointC(x):Type   right adjointfalse:C(0)   Γright adjointtrue:C(1)
2rec(false,false,true)=false:C(0)
2rec(true,false,true)=true:C(1)

Local completeness rule

  

Next Steps

Other types are discussed on the following pages:

 

 

metadata block
see also:
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag Computation and Reasoning - This book is about type theory. Although it is very technical it is aimed at computer scientists, so it has more discussion than a book aimed at pure mathematicians. It is especially useful for the coverage of dependant types.

 

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.