Maths - Exponent (Function) Types

A function type is sometimes called an exponent type. This is related to the way we usually use the term 'exponent' in algebra, for example in sets, the number of mappings from A to B is given by the number of elements in B to the power of the number of elements in A.

Notation

Function Type

ref ncatlab

In type theory a function type can be constructed from(deconstructed to) an expression.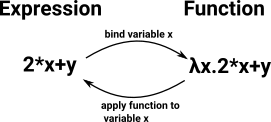

This requires the concept of substitution.

Usually defined as a 'negative type', that is we define it by how it is used (applying a function).

We can think of the type A->B as either,

• All the possible functions from type A to type B (a homset).
• Object of type B parameterised by an variable of type A.

I find it easier to understand the introduction and elimination rules in terms of the second interpretation.

To introduce a term of type A->B we need a free variable in A and a term of type B containing x.

Rules

Types are defined by their formation, term introduction, term eliminator and computation rules:

	Function Type
formation rule Given any two types A and B we can form a function type A->B	A:Type   B:Type A->B : Type
term introduction rule assume a implies b (given a proof of A we get a proof of B)	lambda abstraction: Γ a:Ab:B   ΓB:Type Γλa.b : A -> B
term eliminator Modus Ponens	application: ΓA->B:Type   Γa:A Γf(a) : B
computation rule substitution - in this case of a for x.	( λ x . b(x)) (a) ->β b(a) we reduce this by substitution. b[a/x]
Local completeness rule eta reduction rule	M:A->B ->η λ x. M x

So function terms are introduced using the lambda abstraction. This is a binder which captures a variable (see lambda calculus page).

We eliminate a function term by applying it. In logic this is known as 'modus ponens' that is: given A and a function from A to B we can imply B.

So the term introduction rule binds a variable and the term eliminator removes that variable.

β-reduction and η-reduction

λ a.Φ : A->B

(λ a.Φ) a = Φ
(λ a.Φ) x = [a/x]Φ

f = (λ x . f(x))

β Reduction

β Equality

Two terms are β-equal is one β-reduces to the other one.

M =_βN

if there are terms M₀ to M_n such that M₀M, M_nN and for all i such that 0 ≤i<n

either: M_i =_βM_i+1 or M_i+1 =_βM_i

β-Normal Form

• M is in β-normal form if M does not contain any redux
• M is weakly normalising if there is an N in β-normal form such that M -> _βN
• M is strongly normalising if there are no infinite reduction paths starting from M

Idris Examples

constructExp : Int -> String
constructExp = \ x => prim__toStrInt x

*typeTheory> constructExp
\x => prim__toStrInt x : Int -> String

applyFn : (t1 -> t2) -> t1 -> t2
applyFn f v = f v

*typeTheory> applyFn prim__toStrInt 3
"3" : String

Implemetations of Function Type

||| Function application.
apply : (a -> b) -> a -> b
apply f a = f a
  

We can implement in Idris like this:

Idris> \x => prim__toStrInt x
\x => prim__toStrInt x : Int -> String
Idris> (\x => prim__toStrInt x) 3
"3" : String

Logic

In logic this structure corresponds to 'implication'.

There is an interpretaion of type theory (known as Curry-Howard) that has the same structure as intuitional logic. In this interpretation an element (term) of a type is a proof of that type.

Implication is a bit like taking a whole rule, putting brackets round it and using it as a premise for another rule.

Implication and Modus Ponens

This is discussed further on the propositional logic page.

Alternatively we can represent modus ponens using context () as follows:

C(B => D) C /\ BD

λ-calculus

(see page here)

Here is a reminder of the notation:

Note: although I have used an arithmetic expression above, λ-terms are usually defined in a more abstract way, in the extreme case every term is a function.

T ::= V | (T T) | (λV.T)

where

• V is a variable (a symbol taken from an infinite set of symbols).
• (T T) juxtaposition is function application, different from T(T) notation.

Next Steps

Other types are discussed on the following pages:

• product
• sum
• exponent
• nat num
• bool
• unit

EuclideanSpace

home

Overview

Here we give an example of a type - the exponent (function) type.

For more general information about types see the page here.

Type theory is related the category theory. For information about exponent categories see this page.

Curry-Howard Correspondence

There is a relationship between computer programs and mathematical proofs, this is known as the Curry-Howard correspondence.

A type in λ-calculus has the same mathematical structure as a proposition in intuitionistic logic.

A constructor for that type corresponds to a proof of the proposition. The following table has some specific types with their corresponding propositions:

For more information about the Curry-Howard correspondence see the page here.