Lambda Calculus

In type theory a function type can be constructed from(deconstructed to) an expression.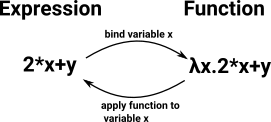

Type Theory rules for Lambda Calculus

	Function Type
formation rule Given any two types A and B we can form a function type A->B	A:Type   B:Type A->B : Type
term introduction rule assume a implies b (given a proof of A we get a proof of B)	lambda abstraction: Γ a:Ab:B   ΓB:Type Γλa.b : A -> B
term eliminator Modus Ponens	application: ΓA->B:Type   Γa:A Γf(a) : B
computation rule substitution - in this case of a for x.	( λ x . b(x)) (a) ->β b(a) we reduce this by substitution. b[a/x]
Local completeness rule eta reduction rule	M:A->B ->η λ x. M x

More about function type constructors (and deconstructors or eliminators) on page here.

Substitution

The computation rule above implements substitution. This computation rule is the term eliminator followed by the term introduction rule.

This is β-substitution, which is a change of the variable name.

• More about binding variables and substitution on the type theory pages.
• More about substitution on the category theory pages.

Next

Modeling Computation

 

EuclideanSpace

home

Modeling Computation