The intuitionisticLogic domain implements a Heyting algebra implied by intuitionistic logic similar to boolean algebra.
Intuitionistic or constructive logic is similar to classical logic but where the law of excluded middle is not used.
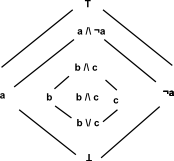
The implementation starts with a 'free logic algebra' that is an algebra where each combination of inputs to /\ , \/ and ¬ generates a new element. So an expression like T /\ T is just T /\ T and does not simplify.
Then by adding "simplification rules" (should I have called them relators?) then other logic algebras can be implemented (intuitional, ternary, many-valued, boolean) just by adding the "rules".
These "rules" are hardcoded into the /\ , \/ and ¬ implementations (rather than implementing a true rule based system).
Simplification rules :
- ~T -> _|_
- ~(~T) -> T
- ~x /\ x -> _|_
- x /\ ~x -> _|_
- x /\ x -> x
- _|_ /\ x -> _|_
- x /\ _|_ -> _|_
- T \/ x -> T
- x \/ T -> T
- x \/ x -> x
- x /\ T -> x
- T /\ x -> x
- x \/ _|_ -> x
- _|_ \/ x -> x
where:
- T = true
- _|_ = false
- x = arbitrary proposition
An option to generalise this code might be to implement the 'free logic algebra' as a category, then intuitional, ternary, many-valued, boolean could be domains which overload /\ , \/ and ¬ with their own sets of rules.
Note: Please be aware that changes may be made in the future to improve and correct intuitionistic logic domain, such as:
- investigate change of meaning of '=' for intuitionistic logic to represent equivalence rather than equality.
- implement more complete algorithm to decide if two (quantifier-free) intuitionistic formulas are equivalent.
Tutorial
If you have an uptodate version of FriCAS then the intuitionisticLogic domain is already installed. The source code is in a file called logic.spad, which is available here.
Download and compile in the usual way. Make sure it is exposed since Axiom/FriCAS was started.
(1) -> )library ILOGIC
ILogic is now explicitly exposed in frame frame1
ILogic will be automatically loaded when needed from
/home/martin/ILOGIC.NRLIB/ILOGIC |
Intuitionistic logic has many possible values: true "T", false "_|_" and infinitely many other values generated by constructs such as inverse. These can be constructed as follows:
(1) -> logicF()
(1) _|_
Type: ILogic
(2) -> logicT()
(2) T
Type: ILogic
(3) -> ~logicT()
(3) _|_
Type: ILogic |
This logic has different rules from boolean algebra and all constructions do not reduce to true or false. To test out our constructs we will use the following list where a and b are independent propositions so that we can check how they interact:
(4) -> l:List ILogic := [logicF(),logicT(),proposition("a")
,~proposition("a"),proposition("b"),~proposition("b")]
(4) [_|_,T,a,~(a),b,~(b)]
Type: List(ILogic) |
First we will try 'not':
(5) -> [(~j)::OutputForm for j in l]
(5) [~(_|_),_|_,~(a),~(~(a)),~(b),~(~(b))]
Type: List(OutputForm) |
We can print a truth table for 'and' and 'or'. This is the same as boolean logic for true/false values and extended for the unproven case.
(6) -> matrix[[(k /\ j)::OutputForm for j in l] for k in l] (6)
Type: Symbol (7) -> matrix[[(k \/ j)::OutputForm for j in l] for k in l] (7)
Type: Symbol |
'implies' produces the following truth table.
(8) -> matrix[[implies(k,j)::OutputForm for j in l] for k in l] (8)
Type: Symbol |
Now that we can do intuitionistic logic with constant values we can go on to represent theories. We can enter a symbolic value as follows:
(9) -> proposition("p1")
(9) p1
Type: ILogic |
When applying a symbolic value, then it may not possible to compress as a single node, so the result remains as a tree. So (13) can be reduced to a single value _|_ because the result does not depend on 'a', however in (12) we cannot reduce to a single value.
(10) -> proposition("a") /\ proposition("b")
(10) (a/\b)
Type: ILogic
(11) -> implies(proposition("a"),proposition("b"))
(11) (a->b)
Type: ILogic
(12) -> proposition("a") /\ logicT()
(12) a
Type: ILogic
(13) -> proposition("a") /\ logicF()
(13) _|_
Type: ILogic |
Applying modus ponens
modus ponens tells us that given: 'a' and 'a->b' then we can imply 'b'. So we first assert 'a' and 'a->b' as follows:
(14) -> givens := proposition("a") /\ implies(proposition("a"),_
proposition("b"))
(14) (a/\(a->b))
Type: ILogic
|
We then factor into seperate terms:
(15) -> fgivens := factor(givens)
(15) [a,(a->b)]
Type: List(ILogic)
|
We now apply the deductions function to this list.
(16) -> deduct := deductions(fgivens)
(16) [b]
Type: List(ILogic)
|
so we get the required deduction 'b'
Intuitionistic logic can be coerced to and from SKI combinators. For a tutorial about how to coerce to/from this algebra see this page.
