- I have put information about my code for HTML formatted output on the page here.
- I have put information about my code for Monospaced formatted output (for output to the command line console) on the page here.
- If you need to use unicode output I have put a simple unicode tester on this page.
Proposal for a Change to The Way FriCAS Formats Output
The remainder of this page explains how FriCAS formats its output and proposes changes to the way that this works.
Why Change?
FriCAS can output mathematical expressions and structures in various formats such as text, TeX, mathML, html and so on. However it is hard to add new formats or change existing formats. There are lots of interesting possibilities for changes to interfaces but changes can be stifled due to the fragile state of existing code.
One of the main reasons for the existing difficulties is that the code is a mixture of 3 languages:
- SPAD
- Lisp
- Bootcode
Swapping backward and forward between SPAD and Lisp is a problem because type information is lost and heavy use has to be made of the 'pretend' instruction which is considered bad practice. Bootcode is obscure and badly documented cross between Lisp and SPAD, for this reason it is very hard to work out what this code does.
There are plans to remove dependence on Lisp and bootcode in FriCAS and so the plan is to rewrite all of this purely in SPAD.
Introduction to Formatting Mathematical Output
There is a dilemma for the designers of a Computer Algebra Program (CAS) regarding the best way to specify the formatting of mathematical entities and expressions.
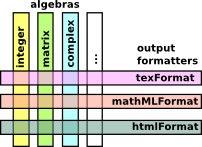 |
We want people to be able to specify new algebras by writing code using SPAD, of course this code will specify the mathematical structure but, how much code should be required to specify what the elements of this algebra will look like when they are displayed on some output device? Each algebra, such as matrix, complex numbers and so on, needs to be displayed in an appropriate way, but how to we specify that? |
In computing, generally, many types of formatter consider it bad practice to mix formatting information in with content. For instance, when writing HTML documents, it is considered good practice to split out the formatting information into Cascading Style Sheets (CSS). This makes the content much more human readable and allows the formatting to be changed without danger of introducing errors.
I guess, in the case of CAS, there is no right or wrong answer. It just depends on what the designers want to optimise. Does the functionality go in each algebra domain, in which case the mathematics code is cluttered with boilerplate code for each output format, or does the functionality go in the drivers which gives less control over the output? Of course, this type of dilemma is not specific to CAS systems (see expression problem on Wiki).
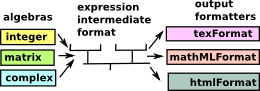 |
The compromise that the SPAD designers came up with is to have an 'intermediate format' for expressions to be output. This contains an expression with all the information semantic structure for doing the mathematical calculations removed and replaced with a presentation structure which specifies how it will be displayed. So, |
- each algebra does not need to know about every formatter.
- each formatter does not need to know about every algebra.
All they both need to know about is the 'intermediate format', which reduces the number of interfaces considerably. But the intermediate format removes semantic structure and replaces it with presentation structure. This removal of semantic structure does put a lot of constraints, on things that it would be otherwise useful to do, as we will see below.
Current Implementation Details
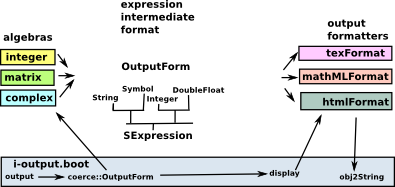
Lets trace through how data gets from each algebra to the data formatters. This is all triggered when 'output' is called in i-output.boot, this then:
- Coerces the algebra to OutputForm (the intermediate format)
- Calls 'display' function on the formatters that are active.
- The formatter may call functions in i-output.boot to help with common processing.
| SPAD domains (algebras) typically have a coersion to OutputForm. Here is an example for complex numbers: | coerce(x : %) : OutputForm ==
re := (r := real x)::OutputForm
ie := (i := imag x)::OutputForm
zero? i => re
outi := '%i::OutputForm
ip :=
(i = 1) => outi
((-i) = 1) => -outi
ie * outi
zero? r => ip
re + ip |
So when we want to output a representation of a complex number then, this code is run, to produce an instance of OutputForm.
Here we get to our first problem: OutputForm and SExpression (see yellow box on right) have a two-way link between them, that is:
Rep of OutputForm is 'SExpression'
and SExpression is
SExpressionOf(String, Symbol, Integer, DoubleFloat, OutputForm)
So, we can't change OutputForm without changing SExpression and visa-versa.
What OutputForm holds is a recursively defined structure which is effectively a tree of lisp types.
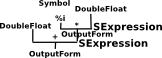 |
So here is an example of the OutputForm structure that might be created for a complex number. What this holds is an intermediate form of an expression in a way that is not specific to any domain and can be understood by all the output formatters. This avoids cross-cut issues, that is, every domain does not need to know specifically about every output format. |
This OutputForm structure then gets passed to the formatters that are active at the time.
These formatters need to do several things:
- Convert this tree structure to text, such as 2 + %i 3.
- This includes adding in brackets where they are necessary.
- Applying any formatting to display correctly (matrix, exponents and so on all require their elements placing in a certain relative position)
- Displaying numbers to the correct number of decimal digits.
Waldek: Use of OutputForm in SExpression can be easily removed: related functions are only used in genufact.spad and fortran.spad. Deeper problem is that fortran.spad apparently assumes that OutputForm = SExpression and passes values to Boot code with little regard to types. Note that defining something like OutputForm2 will help only a little, because code in fortran.spad is supposed to work on OutputForm, so you would need to keep all current mess supporting OutputForm. |
OutputForm
OutputForm is typically constructed in the domain coersions (is there anywhere else it is constructed?) .
The constructors for 'OutputForm' are all well typed, as we can see below, this is then stored in a more messy structure involving 'SExpression'. It also has a disadvantage that every operator symbol, like '+' needs its own constructor built in to Output form, this makes it difficult to add in potential new operators symbols such as: . There are a lot of unicode symbols that would otherwise make the output more readable but are restricted by this mechanism.
. There are a lot of unicode symbols that would otherwise make the output more readable but are restricted by this mechanism.
Waldek: Concerning using more operators, note that all parts involved: coercion to OutputForm and formatters need to know about operators. To allow easy adding of new operators we would need a database storing operator properties, like priority, associativity, how to render it, etc. Currenty we have king of database using mixture of Lisp and Boot, but data is available only to Boot code and can not be used directly by Spad code. We probably also would need to generalize properties of operators, first, there are ordinary infix operators, but then big variants used in prefix form and frequently having some sorts of limits (like summation). |
Here are the constructors for OutputForm, this effectively forms the interface between the domains and the output formatting code:
-- OutputForm constructors
--% Space manipulations
hspace : Integer -> % ++ hspace(n) creates white space of width n.
vspace : Integer -> % ++ vspace(n) creates white space of height n.
rspace : (Integer, Integer) -> %
++ rspace(n, m) creates rectangular white space, n wide by m high.
--% Area adjustments
left : (%, Integer) -> % ++ left(f, n) left-justifies form f within space of width n.
right : (%, Integer) -> % ++ right(f, n) right-justifies form f within space of width n.
center : (%, Integer) -> % ++ center(f, n) centers form f within space of width n.
left : % -> % ++ left(f) left-justifies form f in total space.
right : % -> % ++ right(f) right-justifies form f in total space.
center : % -> % ++ center(f) centers form f in total space.
--% Area manipulations
hconcat : (%, %) -> % ++ hconcat(f, g) horizontally concatenate forms f and g.
vconcat : (%, %) -> % ++ vconcat(f, g) vertically concatenates forms f and g.
hconcat : List % -> % ++ hconcat(u) horizontally concatenates all forms in list u.
vconcat : List % -> % ++ vconcat(u) vertically concatenates all forms in list u.
--% Application formers
prefix : (%, List %) -> % ++ prefix(f, l) creates a form depicting the n-ary prefix
++ application of f to a tuple of arguments given by list l.
infix : (%, List %) -> % ++ infix(f, l) creates a form depicting the n-ary application
++ of infix operation f to a tuple of arguments l.
infix : (%, %, %) -> % ++ infix(op, a, b) creates a form which prints as: a op b.
postfix : (%, %) -> % ++ postfix(op, a) creates a form which prints as: a op.
infix? : % -> Boolean ++ infix?(op) returns true if op is an infix operator,
++ and false otherwise.
elt : (%, List %) -> % ++ elt(op, l) creates a form for application of op
++ to list of arguments l.
--% Special forms
string : % -> % ++ string(f) creates f with string quotes.
label : (%, %) -> % ++ label(n, f) gives form f an equation label n.
box : % -> % ++ box(f) encloses f in a box.
matrix : List List % -> % ++ matrix(llf) makes llf (a list of lists of forms) into
++ a form which displays as a matrix.
zag : (%, %) -> % ++ zag(f, g) creates a form for the continued fraction form for f over g.
root : % -> % ++ root(f) creates a form for the square root of form f.
root : (%, %) -> % ++ root(f, n) creates a form for the nth root of form f.
over : (%, %) -> % ++ over(f, g) creates a form for the vertical fraction of f over g.
slash : (%, %) -> % ++ slash(f, g) creates a form for the horizontal fraction of f over g.
assign : (%, %) -> % ++ assign(f, g) creates a form for the assignment \spad{f := g}.
rarrow : (%, %) -> % ++ rarrow(f, g) creates a form for the mapping \spad{f -> g}.
differentiate : (%, NonNegativeInteger) -> %
++ differentiate(f, n) creates a form for the nth derivative of f,
++ e.g. \spad{f'}, \spad{f''}, \spad{f'''},
++ "f super \spad{iv}".
binomial : (%, %) -> % ++ binomial(n, m) creates a form for the binomial coefficient of n and m.
tensor : (%, %) -> % ++ tensor(a, b) creates a form for a tensor b
--% Scripts
sub : (%, %) -> % ++ sub(f, n) creates a form for f subscripted by n.
super : (%, %) -> % ++ super(f, n) creates a form for f superscripted by n.
presub : (%, %) -> % ++ presub(f, n) creates a form for f presubscripted by n.
presuper : (%, %) -> % ++ presuper(f, n) creates a form for f presuperscripted by n.
scripts : (%, List %) -> % ++ \spad{scripts(f, [sub, super, presuper, presub])}
++ creates a form for f with scripts on all 4 corners.
supersub : (%, List %) -> % ++ supersub(a, [sub1, super1, sub2, super2, ...])
++ creates a form with each subscript aligned
++ under each superscript.
--% Diacritical marks
quote : % -> % ++ quote(f) creates the form f with a prefix quote.
dot : % -> % ++ dot(f) creates the form with a one dot overhead.
dot : (%, NonNegativeInteger) -> % ++ dot(f, n) creates the form f with n dots overhead.
prime : % -> % ++ prime(f) creates the form f followed by a suffix prime (single quote).
prime : (%, NonNegativeInteger) -> % ++ prime(f, n) creates the form f followed by n primes.
overbar : % -> % ++ overbar(f) creates the form f with an overbar.
overlabel : (%, %) -> % ++ overlabel(x,f) creates the form f with "x overbar" over the top.
--% Plexes
sum : (%) -> %
++ sum(expr) creates the form prefixing expr by a capital sigma.
sum : (%, %) -> %
++ sum(expr, lowerlimit) creates the form prefixing expr by
++ a capital sigma with a lowerlimit.
sum : (%, %, %) -> %
++ sum(expr, lowerlimit, upperlimit) creates the form prefixing expr by
++ a capital sigma with both a lowerlimit and upperlimit.
prod : (%) -> %
++ prod(expr) creates the form prefixing expr by a capital pi.
prod : (%, %) -> %
++ prod(expr, lowerlimit) creates the form prefixing expr by
++ a capital pi with a lowerlimit.
prod : (%, %, %) -> %
++ prod(expr, lowerlimit, upperlimit) creates the form prefixing expr by
++ a capital pi with both a lowerlimit and upperlimit.
int : (%) -> %
++ int(expr) creates the form prefixing expr with an integral sign.
int : (%, %) -> %
++ int(expr, lowerlimit) creates the form prefixing expr by an
++ integral sign with a lowerlimit.
int : (%, %, %) -> %
++ int(expr, lowerlimit, upperlimit) creates the form prefixing expr by
++ an integral sign with both a lowerlimit and upperlimit.
--% Matchfix forms
brace : % -> %
++ brace(f) creates the form enclosing f in braces (curly brackets).
brace : List % -> %
++ brace(lf) creates the form separating the elements of lf
++ by commas and encloses the result in curly brackets.
bracket : % -> %
++ bracket(f) creates the form enclosing f in square brackets.
bracket : List % -> %
++ bracket(lf) creates the form separating the elements of lf
++ by commas and encloses the result in square brackets.
paren : % -> %
++ paren(f) creates the form enclosing f in parentheses.
paren : List % -> %
++ paren(lf) creates the form separating the elements of lf
++ by commas and encloses the result in parentheses.
--% Separators for aggregates
pile : List % -> %
++ pile(l) creates the form consisting of the elements of l which
++ displays as a pile, i.e. the elements begin on a new line and
++ are indented right to the same margin.
commaSeparate : List % -> %
++ commaSeparate(l) creates the form separating the elements of l
++ by commas.
semicolonSeparate : List % -> %
++ semicolonSeparate(l) creates the form separating the elements of l
++ by semicolons.
blankSeparate : List % -> %
++ blankSeparate(l) creates the form separating the elements of l
++ by blanks.
--% Specific applications
"=": (%, %) -> % ++ f = g creates the equivalent infix form.
"~=": (%, %) -> % ++ f ~= g creates the equivalent infix form.
"<": (%, %) -> % ++ f < g creates the equivalent infix form.
">": (%, %) -> % ++ f > g creates the equivalent infix form.
"<=": (%, %) -> % ++ f <= g creates the equivalent infix form.
">=": (%, %) -> % ++ f >= g creates the equivalent infix form.
"+": (%, %) -> % ++ f + g creates the equivalent infix form.
"-": (%, %) -> % ++ f - g creates the equivalent infix form.
"-": (%) -> % ++ - f creates the equivalent prefix form.
"*": (%, %) -> % ++ f * g creates the equivalent infix form.
"/": (%, %) -> % ++ f / g creates the equivalent infix form.
"^": (%, %) -> % ++ f ^ g creates the equivalent infix form.
"rem": (%, %) -> % ++ f rem g creates the equivalent infix form.
"quo": (%, %) -> % ++ f quo g creates the equivalent infix form.
"exquo": (%, %) -> % ++ exquo(f, g) creates the equivalent infix form.
"and": (%, %) -> % ++ f and g creates the equivalent infix form.
"or": (%, %) -> % ++ f or g creates the equivalent infix form.
"not": (%) -> % ++ not f creates the equivalent prefix form.
SEGMENT : (%, %) -> % ++ SEGMENT(x, y) creates the infix form: \spad{x..y}.
SEGMENT : (%) -> % ++ SEGMENT(x) creates the prefix form: \spad{x..}. |
Special support for LaTeX
Structures that extend SetCategory have a function specially for formatting them in LaTeX:
latex : % -> String ++ latex(s) returns a LaTeX-printable output
This is the only output type that has special support on a per-domain basis.
As far as I can see this is rarely implemented in a useful way for most domains. This illustrates the problem of putting formatting code in every domain.
Formatters
There are formatters for:
| algebra | mathprintWithNumber (algebraFormat) |
Monospace two-dimensional mathematical output. This is the default in the command line terminal. At the moment this is implemented in boot code in 'i-output.boot'. I am working on an SPAD version of this on page here. |
| tex | texFormat | LaTeX |
| mathML | mathmlFormat | MathML exists in two forms : presentation and content. This implementation only has supports the presentation form. Because this package only has information from OutputForm/SExpression which has had semantic information removed. |
| html | htmlFormat | Not all browsers support mathML so this gives output which can be cut and pasted directly into a web page. The details of this are described on page here. |
| fortran | FORTRAN output | |
| script | formulaFormat | IBM Script Formula Format output The people who have commented on this document (Ralf, Waldek and Andrey) are not aware of anybody using script formula output, so it probably can be safely scrapped. |
| TeXmacs | texmacsFormat texmacs.spad.pamphlet |
For information about TeXmacs see GNU TeXmacs home page |
We can switch between the various formatters by using the ')set output' as follows:
| )set output html on | turn html output on. To command line terminal by default |
| )set output html off | |
| )set output html mypage | This will redirect the html output to a file named mypage.html in the default directory or the directory set by )cd system |
| )set output html console | Switch back to command line terminal (default value) |
Multiple formatters can be active at any time.
As far as I can tell all these formatters are domains (but it looks like some were originally packages). In cases like HTMLFormat and MathMLFormat I cant see what the rep is?
Waldek: AFAICS HTMLFormat, MathMLFormat and TexmacsFormat really are packages. There are no way to create data of those type, so no need for Rep. ScriptFormulaFormat and TexFormat have represetation as records which are used to store prolog and epilog data. IIUC this is because those formats need to send some setup data at start and close data et the end. Trying to put such data around each separate piece of data would be problematic. However, it appears that this functionality is not used by FriCAS, so it seem to be just a little convenience for some users. AFAICS this could be removed from formatters, and if needed provided by generic wrapper. |
Its hard to know what the minimum requirements are for a formatter. They only extend SetCategory so there is not much clue there. As usual with this stuff the documentation is inadequate.
| The main thing the formatters need to export is: | display : String -> Void |
| Although some formatters have: | display : % -> Void |
| Most formatter also have: | coerce : OutputForm -> String |
It would be better if they all had a common interface. That is, it might be better if there were a common category for all formatters which defined their interface in a standard way. For some of these formatters I can't work out what % holds and where its $Rep is defined? (although they are all now domains) .
Comments about TeXmacs by Andrey G. GrozinTeXmacs can be used as a GUI front end for FriCAS, maxima, reduce, sympy, sage, some othes CASs (Axiom, giac, macaulay2, cadabra, yacas, mathemagix, pari, maple, Mathematica, MuPAD, maybe more), as well as to octave, scilab, R, some plotting programs (asymptote, gnuplot) and others - the full list is lengthy. You can open sessions to these CASs from TeXmacs window. It provides high quality of typesetting mathematics (as high as TeX/LaTeX, but interactively). Input for CASs also can be written in a nice typeset 2D form (this requires some translation rules, say, how to send integrals or sums to each CAS; such rule sets are, of course, incomplete, and in many cases a user has to use syntax specific to a given CAS, maybe intermixed with 2D mathematical notation). It is easy to copy-paste, say, a matrix derived in a FriCAS session into an octave session for further numerical work. At the moment, TeXmacs is the best free GUI to mathematical programs. One program should do one thing well; TeXmacs interactively typesets mathematics very well. It seems a waste of time to develop separate (and incompatible) GUI front ends for each CAS. Why not use TeXmacs as the main GUI? Currently, only mathemagix is doing so. It integrates with TeXmacs closely. For example, it has dynamic plots (and other dynamic objects). Say, I have a plot of a function depending on some auxilliary parameters somewhere in a TeXmacs window. I assign a new value to one of these parameters, and the plot immediately changes, without the need to re-run a plotting command. Such level of integration can be achieved in FriCAS, too, but this requires further work. ioHooks are invaluable for implementing interactions of FriCAS with external programs, such as TeXmacs and others. I'd say that the TeXmacs format is one of the most useful ones, because it gives FriCAS an excellent GUI. Also the fortran format is useful for anybody who plans to use derived formulas for an intensive numerical work (it is still done in fortran in many cases). IBM script is, probably, not used anymore. I'd say that making the user experience with TeXmacs (GUI) / FriCAS (engine) even better than it is today is very important. For example, TeXmacs can be an improved replacement for HyperDoc, with a modern and intuitive interface (HyperDoc definitely looks and feels old-fashioned). This can be achieved by doing only a moderate amount of work. This is especially important in today's world where programs without a nice and convenient GUI are considered old-fashioned, and are often not even considered by potential users. Andrey |
Adding in Brackets
When the expression is coded in tree form, no brackets are needed, but when this is linearised into text form then infix operators may need to be bracketed. Whether brackets are needed, or not, depends on operator precedence. For instance, to distinguish between expressions like these:
- a + b * c
- (a + b) * c
There is a need for variable precedence per given operator so, operator precedence needs to be stored in OutputForm for every infix, prefix and postfix operator. For example, '/\' operator for Clifford algebra could have a different precedence to '/\' operator for booleans. (I realise input would have to be done separately).
Displaying numbers to the correct number of decimal digits
FriCAS allows us to change the default output length of numbers, for example:
- digits(49)
Other output formatting commands are,
- outputFloating()
- outputFixed()
- outputGeneral()
There are various things that can be configured using the ')set' command, for example,
| )set expose add constructor OutputForm | |
| )set output length | The maximum width of the output line |
| )set fortran fortlength | except fortran which uses this |
Instead of getting access to these commands by $Lisp calls it would be better to have system calls available directly from SPAD.
interp/i-output.boot.pamphlet
This is where the coerce from the algebra to OutputForm and display$OutputForm functions actually get called. i-output also seems to contain lots of routines which can be called by the various formatters.
Note that, in some cases display(String) is used and in other cases display(%) is used:
| What is 'ioHook' and what is the need for this different version of TeX? | texFormat expr ==
ioHook("startTeXOutput")
tf := '(TexFormat)
formatFn :=
getFunctionFromDomain("convert",tf,[$OutputForm,$Integer])
displayFn := getFunctionFromDomain("display",tf,[tf])
SPADCALL(SPADCALL(expr,$IOindex,formatFn),displayFn)
TERPRI $texOutputStream
FORCE_-OUTPUT $texOutputStream
ioHook("endOfTeXOutput")
NIL |
texFormat1 expr ==
tf := '(TexFormat)
formatFn := getFunctionFromDomain("coerce",tf, [$OutputForm])
displayFn := getFunctionFromDomain("display",tf,[tf])
SPADCALL(SPADCALL(expr,formatFn),displayFn)
TERPRI $texOutputStream
FORCE_-OUTPUT $texOutputStream
NIL |
|
|
mathmlFormat expr ==
mml := '(MathMLFormat)
mmlrep := '(String)
formatFn := getFunctionFromDomain("coerce",mml,[$OutputForm])
displayFn := getFunctionFromDomain("display",mml,[mmlrep])
SPADCALL(SPADCALL(expr,formatFn),displayFn)
TERPRI $mathmlOutputStream
FORCE_-OUTPUT $mathmlOutputStream
NIL |
texmacsFormat expr ==
ioHook("startTeXmacsOutput")
mml := '(TexmacsFormat)
mmlrep := '(String)
formatFn := getFunctionFromDomain("coerce",mml,[$OutputForm])
displayFn := getFunctionFromDomain("display",mml,[mmlrep])
SPADCALL(SPADCALL(expr,formatFn),displayFn)
TERPRI $texmacsOutputStream
FORCE_-OUTPUT $texmacsOutputStream
ioHook("endOfTeXmacsOutput")
NIL |
|
htmlFormat expr ==
htf := '(HTMLFormat)
htrep := '(String)
formatFn := getFunctionFromDomain("coerce", htf, [$OutputForm])
displayFn := getFunctionFromDomain("display", htf, [htrep])
SPADCALL(SPADCALL(expr,formatFn),displayFn)
TERPRI $htmlOutputStream
FORCE_-OUTPUT $htmlOutputStream
NIL |
|
output(expr,domain) ==
if isWrapped expr then expr := unwrap expr
isMapExpr expr =>
if $formulaFormat then formulaFormat expr
if $texFormat then texFormat expr
if $algebraFormat then mathprintWithNumber expr
if $mathmlFormat then mathmlFormat expr
if $texmacsFormat then texmacsFormat expr
if $htmlFormat then htmlFormat expr
categoryForm? domain or domain = ["Mode"] =>
if $algebraFormat then
mathprintWithNumber outputDomainConstructor expr
if $texFormat then
texFormat outputDomainConstructor expr
T := coerceInteractive(objNewWrap(expr,domain),$OutputForm) =>
x := objValUnwrap T
if $formulaFormat then formulaFormat x
if $fortranFormat then
dispfortexp x
if not $collectOutput then TERPRI $fortranOutputStream
FORCE_-OUTPUT $fortranOutputStream
if $algebraFormat then
mathprintWithNumber x
if $texFormat then texFormat x
if $mathmlFormat then mathmlFormat x
if $texmacsFormat then texmacsFormat x
if $htmlFormat then htmlFormat x
(FUNCTIONP(opOf domain)) and (not(SYMBOLP(opOf domain))) and
(printfun := compiledLookup("<<",'(TextWriter TextWriter $), evalDomain domain))
and (textwrit := compiledLookup("print", '($), TextWriter())) =>
sayMSGNT [:bright '"AXIOM-XL",'"output: "]
SPADCALL(SPADCALL textwrit, expr, printfun)
sayMSGNT '%l
-- big hack for tuples for new compiler
domain is ['Tuple, S] => output(asTupleAsList expr, ['List, S])
sayALGEBRA [:bright '"LISP",'"output:",'%l,expr or '"NIL"] |
FriCAS Infrastructure
In addition to the code discussed so far there is a certain amount of plumbing required to make this all happen.
setvart.boot
I have no idea what this file does? It appears to provide various parameters for each output type such as its filename extension. |
(tex
"create output in TeX style"
interpreter
FUNCTION
setOutputTex
(("create output in TeX format"
LITERALS
$texFormat
(off on)
off)
(break $texFormat)
("where TeX output goes (enter {\em console} or a pathname)"
FILENAME
$texOutputFile
chkOutputFileName
"console"))
NIL)
(mathml
"create output in MathML style"
interpreter
FUNCTION
setOutputMathml
(("create output in MathML format"
LITERALS
$mathmlFormat
(off on)
off)
(break $mathmlFormat)
("where MathML output goes (enter {\em console} or a pathname)"
FILENAME
$mathmlOutputFile
chkOutputFileName
"console"))
NIL)
(texmacs
"create output in Texmacs style"
interpreter
FUNCTION
setOutputTexmacs
(("create output in Texmacs format"
LITERALS
$texmacsFormat
(off on)
off)
(break $texmacsFormat)
("where Texmacs output goes (enter {\em console} or a pathname)"
FILENAME
$texmacsOutputFile
chkOutputFileName
"console"))
NIL)
(html
"create output in HTML style"
interpreter
FUNCTION
setOutputHtml
(("create output in HTML format"
LITERALS
$htmlFormat
(off on)
off)
(break $htmlFormat)
("where HTML output goes (enter {\em console} or a pathname)"
FILENAME
$htmlOutputFile
chkOutputFileName
"console"))
NIL)
))
|
How FriCAS Communicates with External Code
| The default interface for FriCAS is the console command line interface. This is hooked up to the other stuff in this document by a messy set of 'C' code. This 'C' code glues this stuff together and does anything that requires multithreading. | 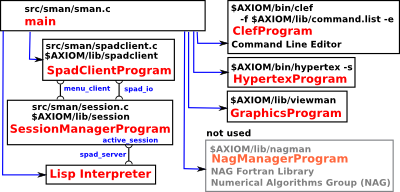 |
There are two other ways to interface to FriCAS:
- TeXmacs
- efricas
I don't know the details of how these interface to FriCAS (TeXmacs seems to have a specific formatter and efricas doesn't).
Ralf has said, as far as he knows, TeXmacs can embed FriCAS in its documents and when one calls fricas from TeXmacs, then fricas outputs in texmacs format and texmacs does the formatting.
This is where the ioHooks (mentioned elswhere in this document) come into play.
I would like to add a two way graphical interface, see 'Graphics Functionality' section below. That is a two way interface to a program written in a language that has rich graphics capabilites such as Java or Python.
Possible Synergy with Aldor?
At the moment the formatting capabilities in Aldor are limited so is there a possibility for FriCAS and Aldor to both use similar standards for their formatting capabilities?
There is a library, called SALLI, which provides Aldor programmers with a extensible computer algebra layer with many low-level functions. Part of this is a stream I/O model which contains an ExpressionTree, described on page here, this has a function very similar to FriCAS OutputForm described above.
I don't know much about Aldor but as far as I can make out (and I might be wrong) there appear to be significant differences:
- Salli seems to be based on 'C' streams. FriCAS does have some clunky old 'C' code with streams but only after all the formatting has been done.
- Although the Aldor/Salli and FriCAS versions are both based on a tree structure the different languages build tree structures in different ways. Salli, like most languages, has different constructs for each type of node and leaf. FriCAS, on the other hand, considers it good practice to crunch all types of node and leaf into a single domain.
- Fricas does most of the work in the formatters, after the expression is removed from the tree. For instance the precedence of operators is compared and decisions about the need for brackets are only taken in the formatter. In Salli decisions about the need for brackets are taken before the tree is built and a flag is put in the tree if brackets are needed.
Possible Enhancements to Functionality
I think it would be really good if this FriCAS code can be put into a state where changes can be made. Some of the changes that I would like are:
- Support in output expressions for operator precedence so, for example, '/\' operator for Clifford algebra could have a different precedence to '/\' operator for booleans. (I realise input would have to be done separately).
- Support in output expressions for graph theory so they know about nodes and edges.
- Make better use of Unicode
Graphics Functionality
FriCAS already has two graphics frameworks but these are for exporting to an output device/file only, they do not allow input as well as output.
I am very keen to have a two-way graphical interface for FriCAS. I would like to work with finite structures but using the command line terminal for this is horrible (Just look at graph theory on page here to see what I mean).
I would like OutputForm to have specific representations of nodes and edges. Of course, they could be coded as strings in the existing structure, but this would involve messy parsing of strings to retrieve the structure.
Eventually this interface needs to bipass the command line altogether. That is a two way interface to a program written in a language that has rich graphics capabilites such as Java or Python.
InputForm
It would be useful if the input to FriCAS could also be built on similar principles to this and even better if they used the same data structures.
Proposed New Rep of 'OutputForm'
I propose that outputForm has the following representation:

This diagram is not complete, it needs to support all the OutputForm constructors shown above, but it does show the level of complexity of the recursively defined structure.
This is a recursively defined structure that no longer uses SExpression and is something less lisp-like, more type-safe and easier to traverse.
Don't forget, this structure is only intended to hold the presentation structure of an expression and semantic structure is only included where it directly affects the appearance. The word 'matrix' is used when perhaps '2D array' might be better, its elements don't have to be numbers and can be strings or anything else.
System Calls
In order to get rid of lisp calls from the proposed SPAD code it would be good if the following system calls were available directly from SPAD to:
- Determine which formatters are currently active.
- Determine the default precedence of any given operator.
- Get all system level data set by such things as digits(n), outputFloating(), outputFixed(), outputGeneral(), ')set output', ')set expose',')set fortran' and so on.
Proposed Changes
The aim is to reduce the dependence on Lisp and boot code, reduce the need for 'pretends' and remove some of the issues mentioned above, so I therefore propose the following changes:
- When an expression is to be output, instead of calling 'output' in 'i-output.boot' new SPAD code (in package?) will be written to replace it: output(domain:Type).
- Make a duplicate of OutputForm called say OutputForm2 and use that in SExpression, this would mean that OutputForm could be changed without affecting any other use of SExpression (or perhaps not - see comments from Waldek above).
- OutputForm to be re-written with a new representation that can be more easily traversed in a safer way without 'pretends' and without any danger of missing any cases that need to be handled.
- All formatters (that it is necessary to keep) need to be modified to use the new OutputForm structure, to replace $Lisp calls by new SPAD code and to fix some messy string handling and similar stuff that has got into some of the formatters.
- A common category for all formatters which defined their interface in a standard way.
Ideally one might like to do these things one at a time. However I think that would be a very inefficient way to do it. I think the hardest part is working out what some undocumented, untyped code is doing and using 'pretends' and so on to get it in the form that is needed. This will be eliminated if we start with the replacement for 'output' in 'i-output.boot' and make the changes following the data path so the code we are working on always has input that is well documented and well typed.
This would be a lot of reworking of code but at the end of it you would have something properly type-safe and Lisp-independent.
Issues
- Need more detail about the ioHook mechanism for interfacing with teXmacs and efricas.
- I have put other issues on my 'wish list' on the page here.