Warning: There is some unfortunate notational overloading here. I'll try to use a capitalised 'Axiom' for the program (any flavour) and lower case 'axiom' for the mathematical concept. I'll try to make the word 'category' clear by the context.
Motivation
There are various ways to divide up mathematics. The Axiom program (here I mean pan-Axiom) generally aligns with these, but there is a slight mismatch.
An Axiom category has little definition of its axioms. Of course a domain must respect its axioms but they are not yet explicitly and automatically policed or available to SPAD or external code. |
 |
I guess we can roughly characterise what is required in a category as
- the function signatures (syntax)
- the axioms (semantics)
It seems to me that It would be very useful to have axioms defined within categories, for many reasons, including such things as:
- Automatically checking of the axioms in domains (if not in real time then at least in test suite).
- As an input to writing compiler-like code in SPAD.
- Support for general equation solver in non-numeric variables.
- Input to a general term rewriting system.
- As a basis for modeling Axiom structures in formal specification tools.
- As an input to theorem provers (either written in SPAD or formal tools)
Gabriel Dos Reis and Yue Li have done a lot of work on specifying axioms in a category and it is starting to appear in OpenAxiom. Three years ago Yue Li used an early version of this for:
- Code generation
- Automatic parallelization
His code is here
and there is some information here.
I would like to help and encourage, in my own small way, putting axiom information in OpenAxiom categories and it seems to me that there is a need to fill the documentation/tutorial holes. I would also like to make information about this available to the Axiom and FriCAS projects in the hope that they might join in.
'assume' Syntax
OpenAxiom and the sandbox code written by Yue Li has gone through some changes and it is not yet completely in its final final form. So its probably best if I try and write down where it is headed but, just to explain existing code, these are roughly the stages:
| Stage 1 - axioms in inline comments in existing categories. |
snippet from here
++ Axioms:
++ \spad{associative("+":(%,%)->%)}\tab{30}\spad{ (x+y)+z = x+(y+z) }
++ \spad{commutative("+":(%,%)->%)}\tab{30}\spad{ x+y = y+x }
AbelianSemiGroup(): Category == SetCategory with |
| Stage 2 - Operator categories added so that axioms can be defined on a per operator basis |
snippet from here
)abbrev category ASSOCOP AssociativeOperator
++ Axiom: associativity: rule op(a, op(b, c)) == op(op(a,b), c)
AssociativeOperator(T: SetCategory, op: Mapping(T, T, T)):Category
== MagmaOperator(T, op) |
| Stage 3 - 'assume' syntax (still on a per operator basis) . |
Snippets from here
SemiGroupOperatorCategory(T: BasicType): Category ==
BinaryOperatorCategory T with
assume associativity ==
forall(f: %, x: T, y:T, z: T) . f(f(x,y),z) = f(x,f(y,z))
and
MonoidOperatorCategory(T: BasicType): Category ==
SemiGroupOperatorCategory T with
neutralValue: % -> T
++ \spad{neutralValue f} returns the neutral value of the
++ monoid operation \spad{f}.
assume neutrality ==
forall(f: %, x: T) .
f(x, neutralValue f) = x
f(neutralValue f, x) = x
|
So extra syntax has been added in to encode the axioms, it would help to have a more precise definition of this extra syntax, here is my first try to reverse engineer the openAxiom syntax (in a semi-formal syntax - not quite the full EBNF to try to make it more readable):
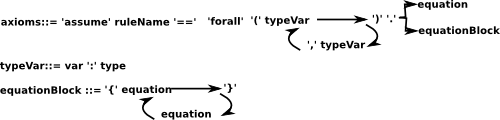
where:
- single quotes means keyword
- '{' means indent (push pile)
- '}' means previous indent (pull pile)
- type is either '%' or type parameter from category parameters.
Using axioms from within SPAD
SPAD does already have a mechanism for specifying rewrite rules (described on the page here. Could this be extended to allow, for instance, identities to be specified as part of each category and domain and to be inherited in the same way that the function signatures are.
It would be useful for:
- A domain to be able to introspect its own axioms.
- Compiler-like SPAD code to be able to read axioms from other categories.
Category Structure
I think there is a need for a way that humans can absorb the complex interrelationship of these structures. Axiom already has diagrams like this It would be good (and I hope useful) to try to extend this to incorporate the axiom information.
In order to explore the possibilities I am starting by using a simple graphical editor (Inkscape) which makes it easier to try out various layouts. The downside, compared to automated methods, is that it it time consuming to maintain and errors can, probably already have, get in.
The first problem is to find the right level of detail. For me, just including the category and domain names does not give enough information to human users about what domains they should use. However too much information makes the diagram cluttered and unusable. I think it will take some experimenting to get the balance right.
Here is a very small sub-diagram (based on catdef.spad.pamphlet) to experiment with layouts and level-of-detail issues:
Here are the operator categories:
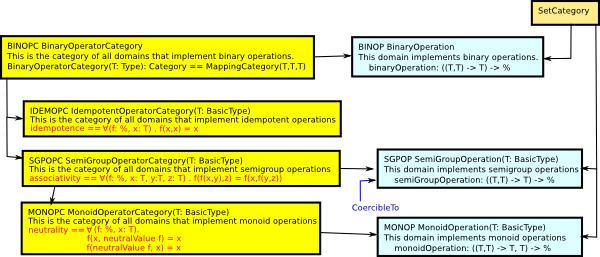
Here are the categories that the operators will be used in.





Key
- black arrows indicate inheritance
- blue arrows indicate coercible to
- it would also be interesting to indicate type constructor parameters as arrows in the diagram (if we think of them as functors then they should conserve some axioms/structure?).
- Yellow boxes are operator categories
- Brown boxes are other categories
- Blue boxes are domains.
- Red text is axioms
- Purple text is axioms (not yet converted)
- Green text is function signatures which are not part of axiom system.
The above diagram is PNG for maximum web browser compatibility but the master is in SVG format here.
I don't know what to do about categories (such as AbelianGroup) that have not been converted yet? Including all function signatures would make the diagram far too big and cluttered but I would like to have function signatures for functions related to axioms. I am concerned that having some function signatures, and not others, could be a source of confusion.
Questions
Here are some unanswered questions that I put on the OpenAxiom forum:
As I understand it, in the existing 'catdef.spad.pamphlet':
Categories that inherit from SemiGroup use '*' as the main operation
*: (%,%) -> %
Categories that inherit from AbelianSemiGroup use '+' as the main operation +: (%,%) -> %
So we can get ring and field-like categories by inheriting from both?
So the commutative axiom is bound up with function names and inheritance details when it might be more flexible if they were independent concepts.
The code in the Yue Li sandbox works differently from this in that it uses a generalised mapping op: Mapping(T, T, T) which can be mixed and matched in a more general way.
I get the impression that the new 'assume' syntax is intended to allow this more generalised approach to be applied to the categories in 'catdef.spad.pamphlet'. I get the impression that each of these mappings would have a category and a domain like this:
- category BINOPC BinaryOperatorCategory
- domain BINOP BinaryOperation
So my questions are:
- q1) Are my above assumptions correct?
- q2) How do you plan to meld this new structure into catdef.spad.pamphlet? Do you plan to replace existing categories one-by-one or build the new structure in parallel with the existing.
- q3) Would all categories in catdef.spad.pamphlet, that represent a single operation over set, also have a domain?
- q4) How would you code a ring-like category to combine two single operation categories?
- q5) Would these new domains add any run-time overhead?
- q6) How to convert logic/rules into axioms/quantifiers, for instance in CancellationAbelianMonoid: c = a+b <=> c-b = a
- q7) Or in EntireRing: ab=0 => a=0 or b=0
- q8) Or in EntireRing: not(1=0)
- q9) Or in OrderedSet: a<b and b<c => a<c
- q10) How would you handle "Conditional attributes" such as in EuclideanDomain: multiplicativeValuation Size(a*b)=Size(a)*Size(b)
- q11) How would you handle constraints like in
Field: a*(b/a) = b | (a not 0)
I Have drawn a diagram (by hand) of all the existing categories in catdef.spad.pamphlet above .
This is just a start, it really needs to be optimised to clarify these issues. Perhaps if I understood the answers to the above questions better I might be able to change it to reflect the proposed new structure?
Formal Methods
Once axioms are more generally included in Axiom then, I think this adds greater potential for interworking with formal methods tools. I therefore think it makes sense to include that topic here. There are many types of such tools available, such as:
- Formal specification programs.
- Formal development programs.
- Formal verification programs.
- Theorem provers.
quote from wiki page:
"In the property-oriented approach to specification (taken e.g. by CASL), specifications of programs consist mainly of logical axioms, usually in a logical system in which equality has a prominent role, describing the properties that the functions are required to satisfy - often just by their interrelationship. This is in contrast to so-called model-oriented specification in frameworks like VDM and Z, which consist of a simple realization of the required behaviour."
So:
- CASL is good at theories (axiom categories).
- ACL2 is good at models of those theories (axiom domains).
(or by Curry–Howard: proofs)
I have not yet seen a program that is good at both.
Gabriel Dos Reis is working on
integration between OpenAxiom and Isabelle. "The first batch of work led
to initial code generators targeting PolyML (one of the primary ML
implementation used for Isabelle). Yue was also involved in that
effort. David Mattews (the main guy behind PolyML) has been very
helpful. More remains to be done."
See also "Calculemus project"
| Tool |
Logic Support |
Configuration Input |
Comments |
| ACL2 |
first order prover |
state machine defined in LISP |
the leader in that field
does term rewriting and proofs. |
| Isabelle |
higher order prover |
axioms |
|
| HOl,
Coq |
higher order prover |
|
based on lambda calculus encoding |
I am planning to experiment with CASL and Isabelle. On this page:
I looked the relation between FriCAS and 'CASL' (an example of an Algebraic Specification Language) and 'Isabelle' (an example of a Proof Assistant).
In particular I looked at how all of these programs code a randomly chosen example - AbelianMonoid. If all these programs were modified slightly to work from a common AbelianMonoid definition then we would get a much richer meta representation.
This site may have errors. Don't use for critical systems.







