The main Axiom/FriCAS code for working with groups is PermutationGroup, this scales well and so is good for working with large groups.
However PermutationGroup is not good for everything so I have written some some other group implementations which are described on the pages linked here:
- Table - Implementation of Cayley Table and Cayley Graph. Because this code does not scale well Waldek does not want to include it in the FriCAS library.
- Presentation - Encode the group as a set of generators and a set of rules. This has been included in the FriCAS library.
There are translations between these and the existing PermutationGroup code such as described in the links here:
- pres->perm - Presentation to Permutation
- perm->pres - Permutation to Presentation
The relationship between presentation and permutation is discussed lower on this page.
Information about PermutationGroup
The original authors provided minimal documentation apart from a reference to a paper:
C. Sims: Determining the conjugacy classes of a permutation group,
in Computers in Algebra and Number Theory, SIAM-AMS Proc., Vol. 4,
Amer. Math. Soc., Providence, R. I., 1971, pp. 191-195
I don't want to try to speak for the original authors but I think it would be useful, for potential users and developers, to have more information in a place where they can find it. (I can't find the above paper online).
I think PermutationGroup is especially in need of documentation bacause the way that mathematitions would describe the subject may not necessarily be seen directly in the code. For example the theory may be derived from stabiliser chains although stabiliser chains may not be directly apparent in the code. Also a lot of the way that the structure is encoded in Rep is not always directly visible to users. Even if you find some information about the Schreier-Sims algorithm, there are a lot of varients of this algorithm so the only way to be sure how it works is to trace though the code.
I did find some other sources for information about the Schreier-Sims algorithm such as this wikipedia page.
Waldek Hebisch referred to these notes by A. Hulpke which contain a sketch of the algorithm.
I have therefore put together this together with what I have worked out myself to attempt this overview of PermutationGroup code.
Introduction
Permutation groups are defined by 2 domains:
- PermutationGroup
- Permutation
Permutation is a domain which can be used to compute permutations. It is also an implementation of Group category.
|
 |
PermutationGroup represents the whole group, that is:
|
 |
So we would expect PermutationGroup to have a representation containing a set (list) of Permutation, it does, but to improve efficiency it also has other information as will be discussed below.
There is a discussion of 'internal' verses 'external' representation of a group on the thread here.
History
The algorithm derives from Schreier's subgroup lemma.
Acording to wikipedia permutation group software developed by Sims led to the proof of existence of some finite simple sporadic groups such as Higman–Sims, Lyons and O'Nan groups. I'm not sure what language that was written in but the SPAD implementation here obviously derived from it.
PermutationGroup Representation
There are many ways to represent a (finite) group, for instance:
- Cayley Table,
- Cayley Graph,
- Permutations,
- Presentation,
- Representation.
These all have advantages and disadvantages, not all of the operations that we might want to do to a given group can be done efficiently in all these forms.
The main way that groups are represented in FriCAS are as permutation groups (although there are domains supporting other forms). The reason is that permutation groups are held in a more compact form and therefore can scale up to bigger groups. The ability to scale is a primary concern in FriCAS.
One reason that permutation groups scale so well is that we do not need to store all the possible elements of the group. Yet we can calculate:
- The order of the group.
- Test permutations to check if they are elements of the group.
- Express elements as words in the group.
without needing to enumerate all the elements.
We store the group as a list of generators in the form of permutations. In order to do the requred operations we need to calculate strong generators and a base for the group. This is stored in Rep so that we only need to calculate it once although it is not independant in that it could be recalculated from the original generators. This additional information is calculated in a function called 'bsgs' see below.
The number of potential Schreier generators is large but highly redundant therefore we can find them more efficiently by generating randomly and then checking that they are correct. This is done in a function called 'bsgs1' see below.
Example 1 - Dihedral Group 3
In order to get some intuition lets look at the dihedral group of dimension 3. This can be defined using 2 generators:
|
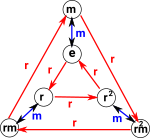 |
Since we are looking at PermutationGroup we can draw it with permutations: The rectangles are intended to show the 3 points and how they are permuted. |
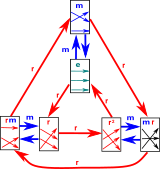 |
Stabiliser Chains
There is a sequence of subgroups which we get by stablising more points. A stabilised point is shown by a horizontal arrow in this diagram (that is, the point is fixed). So G1 is a subgroup of G and stabiliser of the bottom point (fixes the bottom point) and so on to G2...1 |
 |
So this sequence is a bit like gradually resolving some uncertancy as each point in turn gets fixed. We get smaller and smaller subgroups as more points don't move.
So the Stabiliser Chain is a sequence of nested groups:
G > G1 > G2 > ... > Gn
The Schreier-Sims algorithm calculates Gi from Gi+1.
| In our example imagine that we have a solid equilateral triangle with points labled a, b and c: | 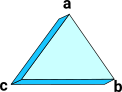 |
We want to find out how many ways there are to slot this into a triangle shaped hole with points labled x, y and z: There are 6 ways to do this, 3 by keeping the same way up and another 3 by flipping top and bottom. |
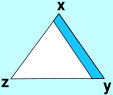 |
| So to choose an orientation for this triangle we can first fix (stabilise) one point, say point 'a' goes to 'z' . | 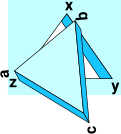 |
| Now that the first point is fixed we can now go on to fix a second point. Say, point 'b' goes to 'y'. This means we have to flip the triangle over. | 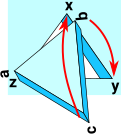 |
So we first chose one of 3 ways that we could have rotated the triangle, then we chose one of 2 ways we could have flipped over or not. This gives 3*2=6 possible orientations for the triangle.
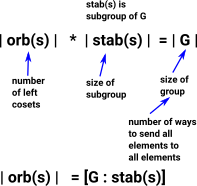
This is an example of the orbit-stabiliser theorem: |orb(s)| * |stab(s)| = |G| where:
|
 |
How to find Stabilisers
We could enumerate all elements of the group and choose those that fix an element but we want to avoid enumerating all elements because this does not scale up. Schreiers lemma allows us to find stabilisers more efficiently.
Stabilisers as Subgroups
If we have a sequence of subgroups, defined by stabilisers, how do they interact? In the diagram on the right we have a group 'G' which acts on a set 'S'. There are two subgroups: Gx which stabilises x and Gy which stabilises y. If there is an element 'g' of G which maps x to y (x and y are in the same orbit) then: combining: g•x = y and h•y = y gives: h•(g•x) = g•x so left multiply by g-1 gives: g-1•h•g•x = x |
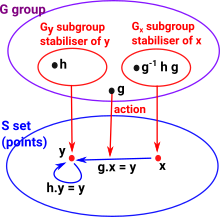 |
so g-1•h•g where h That is the stabilizers of elements in the same orbit are conjugate to each other. |
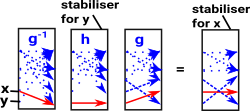 |
Of course g-1•g will also stabilise x, but this is just the identity element, we want a stabiliser for x which does not give trivial group.
Orbit
For all g x->gx Considering the function 'f' from G to the set on which it acts: The image is the orbit of g The coimage is: coimage f = G/ker f |
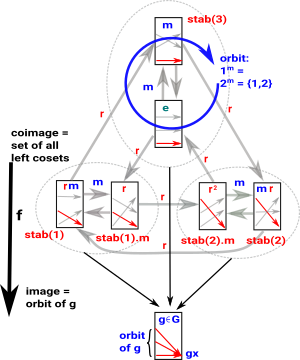 |
Base and Strong Generators
We want to divide the group into a sequence of subgroups but how to we find subgroups that can form such a sequence?
In the example 1 above (D3). Looking at the Cayley diagram there are some obvious candidates for our first subgroup:
- e and m
- e,r and r2
However, we don't choose these, we choose subgroups based on stabilisers and orbits.
| Consider stab(1), this will give us a subgroup, along with some cosets: | 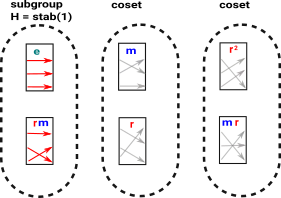 |
We can also slice the elements in a horizontal direction to show the orbits: In this cas we get we get the orbit+svc: [orb = [1,2,3], svc = [-1,1,2]] |
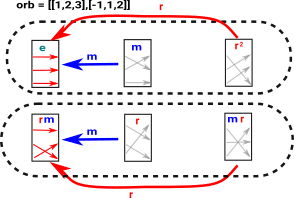 |
Each of these two elements ('e' and 'rm') are a unique representitive element of its coset. They are unique because they have a direct input from each of the other elements of the coset, by 'direct input' I mean by using the original generators 'm' and 'r'.
This is known as a transversal, not every group has this property, however the element can still be unique if the inverse generators still get us closer to each element.
The distinguished set of coset representitives is given by:
h t h-1![]() T for any h
T for any h![]() H, t
H, t![]() T
T
Where T is a transversal for subset (H) in group (G).
Let:
- A base be a sequence of points stabilised by the (sub)groups: G, Gi ..1
- These (sub)groups form a sequence Gi is the ith group in this sequence where G1 is G and Gn is 1.
- We sometimes use H to stand for any subgroup (such as Gi)
- Xi are the generators of Gi
- Ui a set of coset representatives for the cosets of Gi+1 in Gi.
For an element (permutation) g![]() G we can decompose it as ukuk−1...u1 where ui
G we can decompose it as ukuk−1...u1 where ui![]() Ui.
Ui.
We choose a base, by setting Gi+1 as the stabiliser of i+1 in Gi.
To find a set of representatives of the stabiliser use bijection: the quotient of G by the stabiliser of β![]() {1,…,n} is the same as the orbit of β in G.
{1,…,n} is the same as the orbit of β in G.
Schreier’s Lemma
Schreier’s Lemma: given a set of representatives we can calculate a set of generators.
For any g![]() G, let [g] (or sometimes denoted g) be the element of U that represents the coset gH, i.e. [g]H=gH, and [g] lies in U.
G, let [g] (or sometimes denoted g) be the element of U that represents the coset gH, i.e. [g]H=gH, and [g] lies in U.
Then H is generated by the set
{[sr](sr)−1 | r![]() U,s
U,s![]() X}
X}
See wikipedia
Theory tutorials on the web:
Alternative Schreiers Lemma descriptionGα = < ui x uj-1 : 1 ≤ i,j ≤ n , x![]() X, αi • x = αj >
X, αi • x = αj >
where
α • x = { α1 , α2 , ... , αn }
see here
Right Traversal
set T0 =1
set Ti+1 = Ti U (subset of Ti X) that does not contain any redundant representative of the same right coset.
That is: Ti+1does not contain two elements g1, g2 such that αg1 = αg2
Stop when Ti+1 = Ti
Algorithm more efficient when all transversals are computed in parallel.
see transversal
Program Code
Having given an overview of the theory we now go on to discuss the implementation.
Coding a Permutation
There are 2 ways, considered here, to represent a permutation type:
- 'preimage-image' coding.
- 'vector' coding.
More about this on page here.
| PermutationGroup uses vectors as an alternative coding to represent permutations (generators and elements of the group). The elements of these vectors use indexes to represent points. I guess vector terminology makes sense because they transform one set of points into another set of points. However I don't think they are vectors in the sense of being elements of a vector space, that is, operations of vector addition and scalar multipication don't seem to be appropriate. | 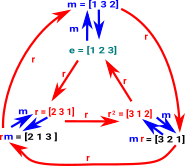 |
The use of the Vector domain for this does seem to be streaching the FriCAS type system a bit. For instance elements of subgroup are coded as a vector of a vector (Vector Vector NNI) which would not be valid if the type system were fully checked but presumably gets away with it because vectors are defined over Type.
So for example:
If a permutation is say (1 2 3) the vector is [2,3,1] this means:
|
If a permutation is say (1 2) the vector is [2,1,3] this means:
|
The local function 'perm_to_vec' creates vectors from permutations.
| Note on terminology: The word 'index' is overloaded on this page. Here we mean replacing underlying set with NNI values but the word 'index' can also have a different meaning when we define number of cosets like this: [G : H]. |
Schreier Vectors (Orbit With SVC)
A Schreier vector (wikipedia) gives additional information about an orbit. A point is either a base point or has information about which generator index will get to it.
In the program the orbit is often strored in the form of: 'orbitWithSvc', this has type : REC ==> Record ( orb : L NNI, svc : V I )
|
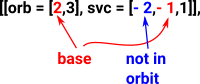 |
This coding has two parts:
- orb : This contains a list of indexes of points of the orbit. The first element in this list is the index of the base point of this orbit
- svc : Schreier vector coded as follows:
A Schreier vector codes its elements like this:
- -2 means point not in orbit,
- -1 means base point
- positive value is index of strong generator moving given point closer to base point.
PermutationGroup Representation
Now we can discuss the representation of PermutationGroup. It holds a list of permutations as we would expect. It also holds extra information of type REC2.
This extra information is not required to define the group, it is only required to make computations more efficient, bacause this information is held in Rep it does not have to be recomputed every time it is used by different functions.
| The representation of PermutationGroup is: | Rep := Record(gens : L PERM S, information : REC2) Where: REC2 ==> Record(order : NNI, sgset : L V NNI, _
gpbase : L NNI, orbs : V REC, mp : L S, wd : L L NNI)
|
So lets see how this is setup in our D3 example:
(1) -> g3 := [[1,2,3] :: Permutation(NNI),[1,2] :: Permutation(NNI)] :: PermutationGroup(NNI)
(1) <(1 2 3),(1 2)>
Type: PermutationGroup(NonNegativeInteger)
This constructs an instance of PermutationGroup with the 'gens' parameter set as shown. However, at this stage, the 'information' data is not set. When a function is called that needs 'information' then the function 'bsgs' will be called which populates information from gens, in this case:
| Information Parameter | Meaning | Value for D3 Example | Type |
|---|---|---|---|
| order | Number of elements. Zero means that 'information' data has not yet been computed. | 6 | NNI |
| sgset | Strong Generators | [[1,3,2],[2,1,3]] | L V NNI |
| gpbase | sequence of points stabilised by the subgroups. | [1,2] | L NNI |
| orbs | Describes orbits of a base point. The orb part is just list of point on the orbit. The svc (see Schreier vector coding above) part allows you to compute element of the group moving given point to base point of the orbit. This list of orbits tends to be in a certain order, (corresponding to the order of gpbase) that is, stabiliser of point 1 (if it exists) is first then the other stabilisers, then the final orbit may not stabilise any points. I don't know if this order is required or assumed by any functions. |
[[orb = [2,3], svc = [- 2,- 1,1]], [orb = [1,2,3],svc = [- 1,2,1]]] |
V REC |
| mp | List of elements of S moved by some permutation (needed for mapping between permutations on S and internal representation) | [1,2,3] | L S |
| wd | Gives representation of strong generators in terms of original generators | [] | L L NNI |
'sgset' - Strong Generators
Fhe local function 'perm_to_vec' is called to convert the generators to 'vectors' as described above.
These vectors are then transformed to have increasing number of stabilisers, that is points where: v(i) = i.
'order'
Number of elements in the group.
If set to zero this means that 'information' data has not yet been calculated in this instance yet.
If a function needs to use the 'information' data it first calls the knownGroup?(gp : %) function, if information.order = 0 then it calls 'bsgs' to set 'gp.information' from gp.gens. Once the information is set further calls to knownGroup? don't need to do anything.
gpbase
list of base points.
orbs
Describes orbits of a base point. The orb part is just list of point on the orbit, base point first. The svc (see Schreier vector coding above) part allows you to compute element of the group moving given point to base point of the orbit.
mp
List of elements of S moved by some permutation (needed for mapping between permutations on S and internal representation).
wd
Gives representation of strong generators in terms of original generators.
Example 1 - Dihedral Group 3
We might think that we could choose a generator that stabilises a point, say 'm' stabilises 3rd point, then split into a (semidirect) product so the first one selects one of the cosets of the second. but thats not how it works. Instead we proceed as follows: Here are the base and strong generators. Note: the generators are notated in the form of vectors (see above) not permutations. |
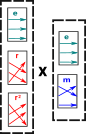 |
| Base | Strong Generators | Orbits |
|---|---|---|
| 1 | [1,3,2] | [orb = [2,3],svc = [- 2,- 1,1]] |
| 2 | [2,1,3] | [orb = [1,2,3],svc = [- 1,2,1]] |
We can see this in FriCAS as follows:
First we create a dihedral group and get base and strong generators for it. |
(7) -> G3 := [[1,2,3] :: Permutation(NNI),[1,2]_
Permutation(NNI)] :: PermutationGroup(NNI)
(7) <(1 2 3),(1 2)>
Type: PermutationGroup(NonNegativeInteger)
(8) -> X3 := base(G3)
(8) [1,2]
Type: List(NonNegativeInteger) |
We calculate the strong generators so the stabiliser chain is: G0 = (2 3),(1 2)
|
(9) -> sgen3 := strongGenerators(G3)
(9) [(2 3),(1 2)]
Type: List(Permutation(NonNegativeInteger))
|
Each of the columns in this matrix represents one of the strong generators. If we apply s to whole group (G) we get the whole group: G = eval(G,s) however no 'g' should be identity, that is for any given 'g' we should not have: g = eval(g,s) for every s. |
(10) -> matrix [[eval(g,s) _
for g in sgen3] for s in [1,2,3]]
+1 2+
(10) |3 1|
+2 3+
Type: Matrix(NonNegativeInteger) |
Example 2 - Symmetric Group 4
Here is another example of base and strong generators, this time for Symmetric Group 4. Note: the generators are notated in the form of vectors (see below) not permutations.
| Base | Strong Generators | Orbits |
|---|---|---|
| 1 | [1,2,4,3] | [orb = [3,4],svc = [- 2,- 2,- 1,1]] |
| 2 | [1,3,2,4] | [orb = [2,3,4],svc = [- 2,- 1,2,1]] |
| 3 | [2,1,3,4] | [orb = [1,2,3,4],svc = [- 1,3,2,1]] |
We can see this in FriCAS as follows:
First we create a symmetric group and get base and strong generators for it. |
(1) -> S : List(Integer) := [1,2,3,4]
(1) [1,2,3,4]
Type: List(Integer)
(2) -> G := symmetricGroup(S)
(2) <(1 2 3 4),(1 2)>
Type: PermutationGroup(Integer)
(3) -> X := base(G)
(3) [1,2,3]
Type: List(Integer)
|
We calculate the strong generators so the stabiliser chain is: G0 = (3 4),(2 4 3),(1 2)
|
(4) -> sgen := strongGenerators(G)
(4) [(3 4),(2 4 3),(1 2)]
Type: List(Permutation(Integer)) |
Each of the columns in this matrix represents one of the strong generators. Again: G = eval(G,s) and no 'g' is identity, that is for any given 'g' we should not have: g = eval(g,s) for every s. |
(5) -> matrix [[eval(g,s)_
for g in sgen] for s in S]
+1 1 2+
(5) |2 4 1|
|4 2 3|
+3 3 4+
Type: Matrix(Integer) |
For S to be a stabiliser chain for all i = {0..n} then S![]() Gi = Gi
Gi = Gi
Where:
- S is entire sequence.
- Gi is ith (sub)group.
so in this case:
- (3 4),(2 4 3),(1 2)
 (3 4),(2 4 3),(1 2) = (3 4),(2 4 3),(1 2)
(3 4),(2 4 3),(1 2) = (3 4),(2 4 3),(1 2) - (3 4),(2 4 3),(1 2)
 (3 4),(2 4 3) = (3 4),(2 4 3)
(3 4),(2 4 3) = (3 4),(2 4 3) - (3 4),(2 4 3),(1 2)
 (3 4) = (3 4)
(3 4) = (3 4) - (3 4),(2 4 3),(1 2)
 Id = Id
Id = Id
Example 3 - Semiregular or Free Action (Id is only Stabiliser)
| Although this example has two generators it does not have a stabiliser and so there is only one base. Note: the generators are notated in the form of vectors (see below) not permutations. |  |
| Base | Strong Generators | Orbits |
|---|---|---|
| 1 | [2,1,4,3],[4,3,2,1] | [orb = [1,2,4,3],svc = [- 1,1,2,2]] |
Notice in 'svc' there are two points that come from generator 2.
| Here we create a permutation group where there are no stabilisers: | (12) -> C1 := coerceImages([2,1,4,3])$Permutation(Integer)
(12) (1 2)(3 4)
Type: Permutation(Integer)
(13) -> C2 := coerceImages([4,3,2,1])$Permutation(Integer)
(13) (1 4)(2 3)
Type: Permutation(Integer)
(14) -> G4 := [C1,C2] :: PermutationGroup(Integer)
(14) <(1 2)(3 4),(1 4)(2 3)>
Type: PermutationGroup(Integer)
|
| So when we generate the base and strong generators there are no subgroups: | (15) -> X4 := base(G4)
(15) [1]
Type: List(Integer)
(16) -> sgen4 := strongGenerators(G4)
(16) [(1 2)(3 4),(1 4)(2 3)]
Type: List(Permutation(Integer)) |
Each of the columns in this matrix represents one of the strong generators. Again: G = eval(G,s) and no 'g' is identity, that is for any given 'g' we should not have: g = eval(g,s) for every s. |
(17) -> matrix [[eval(g,s) for g in sgen4] for s in [1,2,3,4]]
+2 4+
(17) |1 3|
|4 2|
+3 1+
Type: Matrix(Integer) |
Example 4 - Direct Product
Here we create a permutation group with two seperate orbits, that is, the group is a direct product of two cyclic groups.
| Base | Strong Generators | Orbits |
|---|---|---|
| 1 | [1,2,3,5,4] | [orb = [4,5],svc = [- 2,- 2,- 2,- 1,1]] |
| 4 | [2,3,1,5,4] | [orb = [1,3,2],svc = [- 1,2,2,- 2,- 2]] |
A permutation group with two seperate orbits: |
(19) -> C3 := coerceImages([2,3,1,4,5])$Permutation(Integer)
(19) (1 2 3)
Type: Permutation(Integer)
(20) -> C4 := coerceImages([1,2,3,5,4])$Permutation(Integer)
(20) (4 5)
Type: Permutation(Integer)
(21) -> G5 := [C3,C4] :: PermutationGroup(Integer)
(21) <(1 2 3),(4 5)>
Type: PermutationGroup(Integer)
|
| We generate the base and strong generators | (22) -> X5 := base(G5)
(22) [1,4]
Type: List(Integer)
(23) -> sgen5 := strongGenerators(G5)
(23) [(4 5),(4 5)(1 2 3)]
Type: List(Permutation(Integer)) |
(24) -> matrix [[eval(g,s) for g in sgen5] for s in [1,2,3,4,5]]
+1 2+
|2 3|
(24) |3 1|
|5 5|
+4 4+
Type: Matrix(Integer) |
Local function: orbitWithSvc
There is a local function 'orbitWithSvc' which generates an orbit and a Schreier vector from the group from a given base point.
Mathematically the orbit is a set. Here we are calculating the orbit from a given base point so we can use a list with a specific order. The chosen base point is first in the list, the points following it translate into the base point by appliction of the supplied generators and so on.
The Schreier vector has information about which generator to use to get to the base point most quickly.
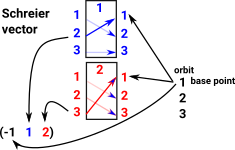
The Schreier vector is generated by working back from the base point as shown in this example for D3:
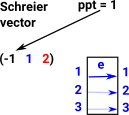
Orbit for point 1 is [1,2,3] Schreier vector for point 1 is (-1,1,2)
|
 |
Orbit for point 2 is [2,1,3] Schreier vector for point 1 is (1,-1,2) In this example both generators could be used to get from base point 2 to point 1 in Schreier vector. So we use generator 1. For generator 2 we instead go to preceeding point in orbit and try generators from there. |
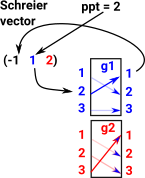
 |
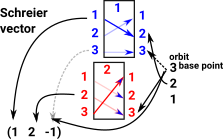
Orbit for point 3 is [3,2,1] Schreier vector for point 1 is (1,2,-1) In this example the point (3) is the stabiliser. So for generator 1 we instead get to preceeding point in orbit which is 2. |
 |
Now we calculate the Schreier vector for one generator only:
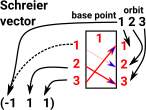
Orbit for point 1 is [1,2,3] Schreier vector for point 1 is (-1,1,1)
|
 |
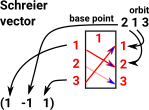
Orbit for point 2 is [2,1,3] Schreier vector for point 1 is (1,-1,1) 2 goes to pint one, to get to point 3 we have to step to next point in orbit. |
 |
Orbit for point 3 is [3,2,1] Schreier vector for point 1 is (1,1,-1) The base point goes through generator to first index, we have to step to next point in orbit to reach the second index. |
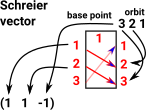 |
And the other generator:
Orbit for point 1 is [1,2] Schreier vector for point 1 is (-1,1,-2) No points in orbit can get back to the third index. |
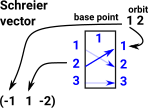 |
Orbit for point 2 is [2,1] Schreier vector for point 1 is (1,-1,-2) |
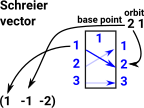 |
Orbit for point 3 is [3] Schreier vector for point 1 is (-2,-2,-1) In this example the point (3) is the stabiliser it cant be reached from any other points. |
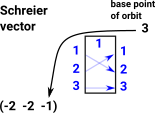 |
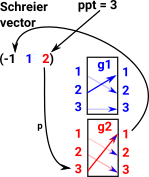
So a Schreier vector depends on:
|
 |
Local function CosetRep1
The local function 'cosetRep1' uses the Schreier vector generated above to calculate the coset representative from the orbit. The representative is a group element (permutation in the form of a vector), not necessarily a generator.
The element we want is an element that returns given point to the base point. That is, given 'ppt' return 'g' such that:
eval(g,ppt) = base point
For example given Schreier vector (-1,1,2) :
If we choose point 1 then looking this up in Schreier vector gives -1. This means that we are already at base point. So just return identity element. |
 |
If we choose point 2 then looking this up in Schreier vector gives generator 1. Applying gen 1 to point 2 gets us to base point so return gen 1. |
 |
If we choose point 3 then looking this up in Schreier vector gives generator 2. Applying gen 2 to point 3 gets us to base point so return gen 2. |
 |
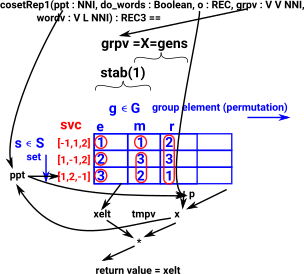 |
Local function 'strip1'
This function maps elements to a representitive element in the same coset. Should this function be called 'CosetRep' instead of the function described above? The stabiliser of point 1 defines a subgroup. In example 1 this is the group containing:
To get the cosets for this group we construct the orbit and then apply cosetRep1 above for each point. |
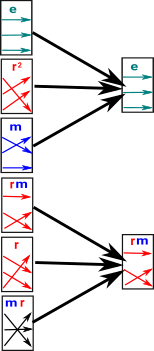 |
bsgs
This is a local function to initialise base and strong generators in %.
Functions such as initializeGroupForWordProblem or knownGroup? are called to make sure 'information' has been initialised in %. If initialation is required then bsgs is called to do the work.
Note: this function calls bsgs1 which uses Monte Carlo methods (random sampling) and so may not give the same result for given parameters.
returns sizeOfGroup but real purpose is side effect of setting 'information' in %.
parameters are:
- group is this instance.
- wordProblem is true if we want to initialise for wordProblem.
- maxLoops if zero then calculate from the (approximate) base length
- diff if word problem then subtract this from maxLoops.
Here are some examples: Dihedral Group 3:
| Base | Strong Generators | Orbits |
|---|---|---|
| 1 | [1,3,2] | [orb = [2,3],svc = [- 2,- 1,1]] |
| 2 | [2,1,3] | [orb = [1,2,3],svc = [- 1,2,1]] |
Here is another example for Symmetric Group 4:
| Base | Strong Generators | Orbits |
|---|---|---|
| 1 | [1,2,4,3] | [orb = [3,4],svc = [- 2,- 2,- 1,1]] |
| 2 | [1,3,2,4] | [orb = [2,3,4],svc = [- 2,- 1,2,1]] |
| 3 | [2,1,3,4] | [orb = [1,2,3,4],svc = [- 1,3,2,1]] |
bsgs1
Local function used by bsgs
Tries to get a good approximation for the base points which are put in gp_info.gpbase and stabiliser chain which is returned in 'out' parameter reference.
These values can be used by bsgs to compute the strong generators but this output may contain duplicates and so bsgs must remove these.
This function is recursive, it calls itself for every subgroup.
Note: this function uses Monte Carlo methods (random sampling) and so may not give the same result for given parameters.
returns sizeOfGroup and sets reference values 'out' (stabiliser chain) and 'outword' if used and also sets gp_info.gpbase (sequence of points stabilised by the group).
parameters are:
- group holds permutations as vectors as they are easier to work with.
- number1 initial index for calculating orbits. bsgs1 is first called with number1 set to '1' but when called recursively it will be incremented so that earlier stabilisers will not be checked again.
- words
- maxLoops if zero then calculate from the (approximate) base length.
- gp is this instance.
- diff if word problem then subtract this from maxLoops.
- out Reference to stabiliser chain which can be appended by this function. The first value stabilises most points, next value less points and so on.
- outword Reference to words (if used) for stabiliser chain.