Finite Group Presentation

In this domain we want to represent finitely generated group presentations, that is, groups represented by their generators and relations.

The code is avialible on Github here.

My motivation is to represent homotopy group such as fundamental group. For more documentation see page here.

The domain representation holds the group as a pair:

a set of generators
and a set of relations

Rep := Record(gens:PrimitiveArray(NNI),rels: List(List(Integer)))

Which is shown like this: <A,B | A , B>

Each generator is a NNI
Each relation is a list of indexes to generators. Negative values indicate
the inverse of the generator. So if '1' represents the generator 'A' then
'-1' represents its inverse 'A^-1'

Working with Group Presentations

Finitely presented group presentations are difficult to work with:

It is not, in general, algorithmically computable into other representations of a group.
We cannot determine if this is the simplest representation or determine if two such groups are isomophic (their corresponding simplicial complexes are homeomorphic).

We can therefore compute 'a' (not 'the') homotopy group for a given simplicial complex. We may also be able to apply some simplifications to this group.

Despite these fundamental limits on what is theoretically possible I still believe it is worthwhile to have the capability to generate 'a' homotopy group for a given structure.

Simplify

There may not be a simplest form but it is possible to do some simplifications.

In order to try to simplify a finitely generated presentation to produce simpler but isomorphic groups we can apply certain transformations or automorphisms (isomorphisms of the group back to itself).

For example:

remove all zero terms in rules
if a rule consists of a single generator then remove that generator
if a rule consists of a pair of generators then make the second generator the inverse of the first
if a generator is adjacent to its inverse then cancel them out.
remove duplicate rules.

These automorphisms were studied and categorised by Tietze and Nielsen.

Tietze Transformations

Tietze transformations are of 4 kinds:

	Kind	Examples
T1	Add a relation	< A \| A³ >->< A \| A³ , A⁶ >
T2	Remove a relation	for example we can reverse the above < A \| A³ , A⁶>->< A \| A³>
T3	Add a generator	< A \| A³ >-><A , B \| A³, B = A² >
T4	Remove a generator	for example we can reverse the above <A , B \| A³, B = A² >->< A \| A³ >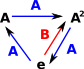

We are interested in simplifying so we are mostly interested in T2 and T4.

T2

T2 allows us to remove a relation but not generators. This happens when a rule is redundant, that is it contains no additional information than is already contained in the other rules.

This happens, for example, where:

One rule is a multiple of another - In this case we can remove the highest multiple but not the lowest.

One rule is the inverse of another - In this case we can remove any one, but not both of these rules.

We can also simplify rules, for example, where an element and its inverse are next to each other they can be cancelled out and removed.

T4

T4 allows us to remove a generator and corresponding rules.

Nielsen Transformations

The following transformations on a finitely generated free group produce isomorphic groups.

Switch A and B
Cyclically permute A, B, … to B, …, A.
Replace A with A^-1 : That is invert any element.
Replace A with A*B

Group domains in FriCAS

Subject: Re: [fricas-devel] Group domains in FriCAS
To: fricas-devel@googlegroups.com
Date: Tue, 6 Dec 2016 15:42:00 +0100 (CET)
From: Waldek Hebisch

Martin Baker wrote:
>
> My initial thoughts about group domains related to homotopy in FriCAS is 
> that there is a need for at least 4 group domains shown at each corner 
> of this square:
>
> PermutationGroup <-----equivalent-----> GroupPresentation
>        |                if finite               |
>        |                                        |
>    contains set of                        contains set of
>        |                                        |
>        V                                        V
> Permutation <-------------------------------> Word
>
> The domains at the bottom of the diagram are implementations of Group 
> category. So in these cases % will contain something representing a 
> single element of the group such as a single permutation or a single 
> word. Functions will be from Group such as '*'.
>
> The domains at the top of the diagram have % which holds information 
> about the whole group so it identifies it as say 'cyclic group 5' or 
> 'dihedral group 3'. The functions will be functions on the whole group 
> such as: sum, product, quotient, subgroup, order, orbit, etc.
>
> (I don't think Bill likes this way of describing it? I think the 
> distinction is valid but can you think of a more mathematical way to 
> describe the distinction? Perhaps in terms of initial and terminal 
> algebras?)
>
> So how does FinitelyPresentedGroup fit in this? It seems to me that 
> FinitelyPresentedGroup is of type: Type whereas GroupPresentation is of 
> a specific type:
>
> (1) -> F:=FPG([x,y,z],[])
>
>     (1)  FinitelyPresentedGroup([x,y,z],[])
>                                                    Type: Type
>
> (2) -> F2 := groupPresentation([1,2,3],[])
>
>     (2)  
>                                        Type: GroupPresentation
>
> Given this, is it possible to construct functions like sum, product, 
> quotient, subgroup, order, orbit, etc. on something of type: Type?
>
> If it is possible to do this, why is PermutationGroup not constructed 
> this way?

Hmm, there are several ways to look at group.  First you can
look at groups as objects (that frequently happens in homological
algebra).  Within such point of view you may consider various
notion of equivalence/equality.  Plain equality is of limited
use, as we may get entirely trivial differences.
Isomorphism is important, but sometimes we need more coarse
equivalence relation, sometimes we need more than isomorphism.
Quite a lot of things done at this level in not computable:
there are various results but very little algorithms.

Treating groups as objects is frequently bundled with categorical
approach: there are various categories and people build
functors from those cateries to groups (or diagrams of groups).

Another point of view is that groups are sets with specific
operations: in FriCAS this is expressed by Group.  There
is some intermediate levels: one can look at say subgroups
of given group or group representations.

Now, for finite groups subgroup is the same as fintely
generated subgroup, so one can represent subgroups
via (finite) sets of generators.  In this sense
PermutationGroup implements subgroup of permutation group
(for given parameter we get single subgroup, while
varying parameters we get all of the subgroups).
In similar spirit we could have MatrixGroup for
subgroup(s) of matrices.  We could also look at
subgroups of free group, but that is less interesting
because subgroup of free group is again a free group. 

In principle for finite groups we could easily represent
quotients, but here is a little catch: if we represent
subgroup via generators, then testing elements of
a group for membership in a subgroup may be tricky
(for infinite groups membership in a subgroup is
undecidable).  In other words, we can only do
things which are efficiently computable.  This
largely explains why PermutationGroup has its
current form: there is efficient algorithms which
uses specific _representation_ of permutations.
This algorithm is efficient _only_ for permutation
groups, trying to treat other groups as permutation
groups would lead to quite inefficient method.
Nowadays there are algorithms which obtain similar
results for matrix groups, but they use specific
properties of matrices.

I have to finish now, I will later write more about
your proposal.

Subject: Re: [fricas-devel] Group domains in FriCAS
To: fricas-devel@googlegroups.com
Date: Wed, 7 Dec 2016 02:01:20 +0100 (CET)
From: Waldek Hebisch

About your proposal: note that notion of permutation
group is closely related to notion of subgroup (and
at categorical level with final object of a category).
Finitely presented groups are related to quotients
(and first object of a category).  As a little remark
note that in both cases we natuarally get semigroup
first, in case of permutations semigroup of all mappings
from a set to itself, in case of free group we get
free semigroup.  Then we "correct" deficiency, in
case of permutations taking subsemigroup of
invertible maps, in case of free group taking
quotient (declaring some generators of free semigroup
as inverses of group generators).

Now, one natural thing would be a way to produce group
given group presentation.  There is very strong
obstacle to this due to unsolvability of word problem.
IMO the right way to go forward it to look at cases
when word problem is solvable.  This happens if
we know something special about groups, for example
for abelian groups word problem is solvable.  This
happens if presentation has special form, like
for result of Knuth-Bendix completition.  We could
try postpone solving hard problems and require that
to create finitely presented group the user has
to provide solver for word problem

Concerning structure on Type: currently this is done by
declaring specific categories/domains.  Union represets
/implements sum.  There is Product domain.  There is
Subdomian.  Each are very special I do not see how
to "generalize" them at computational level.  In principle
we could try to add "quotient" constructor.  Namely,
to get quotient we need equvalence relation and we could
have something like:

Quitient(S : Type, = : (S, S) -> Boolean) : ....

but that would be of limited use, because for products
there are important features which are preserved, while
for quotients everything depends on equivalence relation.
Existing algebra cheats in some cases, uncoditionaly
declaring features which are valid only if special
conditions are satisfied.  For quotient I do not
think cheats are appropriate -- we can not even claim
that features are preserved "in most interesting cases".
And I would like to get rid of cheating. 

Orbits need extra structure for example semigroup structure.
Orbits of group actions have specific properties, so
they probably should be studied separately from more
general notions of orbits.  And efficient computations
with orbits are possible only in some specific situations.

So no, I think that currently it is not possible to put
more _useful_ general structure on Type.

Finite Group Presentation

Working with Group Presentations

Simplify

Tietze Transformations

T2

T4

Nielsen Transformations

Group domains in FriCAS

References

EuclideanSpace

Computer Algebra Systems

Other Code

metadata block

see also:
Correspondence about this page