Maths - Combinatory Logic

This was introduced by Moses Schnfinkel and Haskell Curry with the aim of eliminating the need for variables in mathematical logic. It is equivalent to lambda calculus but it can be used for doing, without variables, anything that would require variables in other systems.

Operators

We can think of functions as taking some 'value' and modifying it in some way to give a potentially different value. Operators raise this up a level so functions become the elements and operators act on the functions.

There are many examples of operators in mathematics, for example in calculus, integration and differentiation take a function and return a different, but related, function.

As the name 'combinators' suggests here we are interested in the ways that existing functions can be combined to produce new functions. For example, a possible way to combine two functions is function composition, that is: if we have two functions f and g then we can combine them by applying f first and then applying g to the output of f (provided the types are compatible of course). Here are some possible ways to combine functions:

Operator	What it does	Expression	Lambda Equivalent	SKI equivalent (normal form)
I	Identity (leave unchanged)	I(f) = f	λx.x Ix->x	I or SKK or SKS
B	Function composition	(B(f,g))(x) = f(g(x))	λxyz.x(yz)	S(KS)K
B'	Reverse function composition	(B'(f,g))(x) = g(f(x))	λxyz.y(xz)
C	Swap functions	(C(f))(x,y) = f(x,y)	λxyz.xzy	S(K(SI))K
K	Form constant function	((K f) g) = f	λxy.x Kxy->x	K
S	Generalized composition	(S f g x) = f(x,g(x))	λxyz.xz(yz) Sxyz->xz(yz)	S
W	Doubling or diagonalizing	(W(f))(x) = f(x,x)	λxy.xyy

Where:

• x,y,z: are elements
• f, g, h: are functions on those elements
• upper case letters are operators

Simplifying Operator Expressions

Often what we want to do is separate out the elements x,y,z so we get something like this:

O (x,y) = P (x,y)

Where O and P are some combination of operators and functions.

So that we can effectively cancel out the elements:

O = P

So we have stepped up a level and are operating purely in terms of functions. When discussing this for functors on the category theory pages we described this as 'lifting'.

An example of this is the axioms of algebra such as the commutative law, usually this is written in terms of arbitrary variables like this:

(x,y)

x + y = y + x

Or if we use + as a prefix rather than an infix operator:

(x,y)		+(x,y) = +(y,x)
		+(x,y) = (C+)(x,y)

Where C means: swap functions as explained in the table above.

So we can cancel out the elements (x,y) and just represent the commutative axiom as:

+ = C(+)

So using operators we don't have to describe axioms in terms of arbitrary elements.

redex is short for reducible expression

Combining Combinators

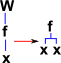
So far we have applied combinators to functions and elements. But how do the combinators interwork? I find it helps to think of combinators as modifiers of a tree structure. In this tree structure elements (x, y ...) are leaves of the tree, functions may either be leaves or nodes. So in this system the combinators look like this:

tree diagram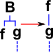
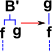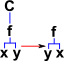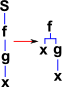expression	IX=X				KXY = X	SXYZ =(X Z(Y Z))

So in this system, how do we represent multiple combinators such as: SKK?

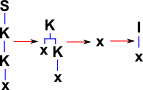((S K K) x) = (S K K x) = (K x (K x)) = x

So here we have used the following conventions:

	Diagram Notation	Text Notation
function call:		(f x) the function is shown as the first symbol inside the brackets, in this case 'f'.
parameters for function :		(f x y) the parameters are the second and remaining symbols inside the brackets, in this case 'x' and 'y'.
function composition:		(f (g x)) here f is applied to the result of the inner function g. So 'g x' is distinguished from being two parameters of 'f' by the inner brackets.
default precedence:		if we have no brackets, for example: A B C then this implies brackets from the left: (A B) C That is A is applied to B and the result of this is applied to C. If we want A to be applied to the result of B applied to C then we must explicitly include the brackets like this: A (B C) Also, if we want B and C to be parameters for A then we must explicitly include the brackets around the whole function, like this: (A B C)

Example - Equivalent SKI sequence for C

C x y =S(K(SI))K x y =K(SI)x(Kx)y =SI(Kx)y =Iy(Kxy) =Iyx =yx

The Curry-Howard Isomorphism

	Combinatory Logic	Intuitional Logic
logic	types (function type signatures)	theorems
programs	programs (typed lambda term)	proofs of those theorems

This gives an isomorphism where theorems in intuitionistic logic correspond to type signatures in combinatory logic and programs in intuitionistic logic correspond to the proofs of those theorems in combinatory logic.

More about Curry-Howard on page here.

K and S Combinators

Here are some combinators, all others can be derived from K and S.

Sometimes known as SKI calculus.

Combinator	Function Definition	Type Signature (Axiom)
I = identity	(I x) = x for all terms x	do nothing (leave unchanged)
K	((K x) y) = x	manufactures constant functions (for any argument, return x): K: A -> (B -> A)
S	(S x y z) = (x z (y z))	generalized version of application S applies x to y after first substituting z into each of them. Or put another way, x is applied to y inside the environment z. S: (A -> (B -> C)) -> ((A -> B) -> (A -> C))
MP		function application corresponds to the detachment (modus ponens) rule: from A and A -> B infer B

I and MP are not strictly necessary because all types can be represented with come combination of S and K. for example I is equivalent to:

((S K K) x)
    = (S K K x)
    = (K x (K x))
    = x

These are only 'equivalent' not 'equal' or 'identical' because they produce the same result for the same arguments but they are not the same.

De Bruijn index

SKI Operator	λ-calculus	De Bruijn index
K	λx. λy. x	λ λ 2
S	λx. λy. λz. x z (y z)	λ λ λ 3 1 (2 1)

Related Subjects

• Category Theory and Natural Transformations
• Lambda Calculus

Next

Modeling Computation

 

EuclideanSpace

home

Prerequisites

Combinatory Logic deals with functions and so is related to:

• Lambda Calculus

Related Subjects

• Proof
• Implementing Logic using FriCAS/Axiom computer algebra system.

Logic Notation

Writing Logic Code Using a CAS Program

Modeling Computation

Curry-Howard Correspondence

There is a relationship between computer programs and mathematical proofs, this is known as the Curry-Howard correspondence.

A type in λ-calculus has the same mathematical structure as a proposition in intuitionistic logic.

A constructor for that type corresponds to a proof of the proposition. The following table has some specific types with their corresponding propositions:

Proposition	Type
true formula	unit type
false formula	empty type
implication	function type
conjunction	product type
disjunction	sum type
universal quantification	generalised product type (? type)
existential quantification	generalised sum type (? type)

For more information about the Curry-Howard correspondence see the page here.