If you have not already done so I suggest you read the page about Simplicial Complexes first and also general introduction here.
Homology is an equivalence between cycles in a topological space. On this page we look at code to test this equivalence.
| When we looked at the delta complex we got a chain of 'face maps' between each dimension and the next lower one. |  |
In homology we treat this as a chain of abelian groups.
| The homology at each step in the chain measures the connectivity of the space. |  |
Matrix Form of Face Maps
We can represent these face maps by matrix representations, this allows us to relate to linear algebra methods.
We can then generate the homology by putting them in Smith normal form (which is already implemented in Axiom/FriCAS).
Example for Tetrahedron
| Here are the face maps as discussed on the delta complex page here. | 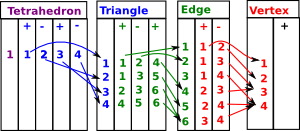 |
We can convert this to a matrices as follows:
| Face map | Matrix | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| δ3 = tetrahedron to triangles |
|
||||||||||||||||||||||||||||
| δ2 = triangles to edges |
|
||||||||||||||||||||||||||||
| δ1 = edges to vertices |
|
For these face maps to be valid chain they must be:
- Composible - number of columns in δ1must equal number of rows in δ2.
- Product is zero - δ1* δ2 = 0
Orientation and Notation
Getting a consistent orientation naming/numbering is very important. We therefore need to take some time to define it precisely
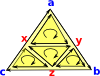
Lets start with a 2-dimensional face, that is, a triangle: Here it is denoted [a,b,c]. It is oriented, that is, as it is drawn here it has a clockwise orientation. An anti-clockwise triangle such as [a,c,b] can be thought of as an inverse. Here we will denote the edges as bc, ca and ab but it is easier if the nodes are alphabetically ordered, so instead we denote the edges: bc, -ac and ab So now each edge is designated in alphabetical order and the middle edge is negative. |
 |
We can subdivide the triangle by adding another node 'x' as shown in the diagram: This allows us to create 3 triangles. Provided that each of these has a clockwise orientation then, The external edges will have the same direction as the original triangle. The internal edges will each have two edges in opposite directions, so we can think of them as canceling out, leaving us with the original triangle. So, [a,b,c] = [b,c] - [a,c] + [a,b] Designating the triangles in terms of their edges we have: [bc, -ac , ab ] = |
 |
In theory we could divide each triangle up into 4, by splitting each edge, like this: However we don't tend to use this method because:
|
 |
Interpreting SmithNormalForm
| Smith normal form is calculated from the face maps in linear algebra (matrix) form. The rows and columns are added and subtracted by multiples to get as much as possible of the matrix in leading diagonal form. | b1 |
0 | 0 | 0 | |
| 0 | b2 | 0 | … | ||
| 0 | 0 | b3 | |||
0 |
0 | ||||
Once in this form we interpret it as follows:
H = Z b1 Z b2
Z b2 Z b3
Z b3 …
…
Calculated Examples
Here are FriCAS examples for common topologies:
If this is different from other CAS programs it may be because they use 'reduced homology' where component of dimension 0 is n - 1 copies of Z. The code here does not use reduced homology.
Disc (filled in circle) an 2-sphere examples
Gives H0=Z, H1= 0, H2 = 0 which we represent as: [Z,0,0] |
(1) -> DCF := DeltaComplexFactory(Integer)
(1) DeltaComplexFactory(Integer)
Type: Type
(2) -> SCF := SimplicialComplexFactory(Integer)
(2) SimplicialComplexFactory(Integer)
Type: Type
(3) -> S := sphereSolid(2)$SCF
(3) points 1..3
(1,2,3)
Type: FiniteSimplicialComplex(Integer)
(4) -> homology(S)
(4) [Z,0,0]
Type: List(Homology) |
Sphere and Disc Surface (Boundary) Example
gives H0=Z, H1= Z, Hn = 0 {n>1}
[Z,Z] |
(5) -> cD := circle()$DCF
(5)
1D:[[1,- 1]]
0D:[[0]]
Type: DeltaComplex(Integer)
(6) -> cS := sphereSurface(2)$SCF
(6) points 1..3
(1,2)
-(1,3)
(2,3)
Type: FiniteSimplicialComplex(Integer)
(7) -> homology(cD)
(7) [Z,Z]
Type: List(Homology)
(8) -> homology(cS)
(8) [Z,Z]
Type: List(Homology) |
Dunce Hat Example
[Z,0,0] |
(9) -> dhD := dunceHat()$DCF
(9)
2D:[[1,1,- 1]]
1D:[[1,- 1]]
0D:[[0]]
Type: DeltaComplex(Integer)
(10) -> dhS := dunceHat()$SCF
(10) points 1..8
(1,2,8)
(2,3,8)
(3,7,8)
(1,3,7)
(1,2,7)
(1,6,8)
(1,2,6)
(6,7,8)
(2,4,6)
(5,6,7)
(2,5,7)
(4,5,6)
(2,3,4)
(2,3,5)
(1,3,4)
(1,4,5)
(1,3,5)
Type: FiniteSimplicialComplex(Integer)
(11) -> homology(dhD)
(11) [Z,0,0]
Type: List(Homology)
(12) -> homology(dhS)
(12) [Z,0,0]
Type: List(Homology) |
Torus example
[Z,Z*2,Z] |
(13) -> tD := torusSurface()$DCF
(13)
2D:[[1,2,- 1,- 2]]
1D:[[1,- 1],[1,- 1]]
0D:[[0]]
Type: DeltaComplex(Integer)
(14) -> tS := torusSurface()$SCF
(14) points 1..7
(1,2,3)
(2,3,5)
(2,4,5)
(2,4,7)
(1,2,6)
(2,6,7)
(3,4,6)
(3,5,6)
(3,4,7)
(1,3,7)
(1,4,5)
(1,4,6)
(5,6,7)
(1,5,7)
Type: FiniteSimplicialComplex(Integer)
(15) -> homology(tD)
(15) [Z,Z*2,Z]
Type: List(Homology)
(16) -> homology(tS)
(16) [Z,Z*2,Z]
Type: List(Homology) |
Real Projective Space Example
[Z,C2,0] |
(17) -> ppD := projectiveSpace(2)$DCF
(17)
2D:[[1,1]]
1D:[[1,- 1]]
0D:[[0]]
Type: DeltaComplex(Integer)
(18) -> ppS := projectiveSpace(2)$SCF
(18) points 1..6
(1,2,3)
(1,3,4)
(1,2,6)
(1,5,6)
(1,4,5)
(2,3,5)
(2,4,5)
(2,4,6)
(3,4,6)
(3,5,6)
Type: FiniteSimplicialComplex(Integer)
(19) -> homology(ppD)
(19) [Z,C2,0]
Type: List(Homology)
(20) -> homology(ppS)
(20) [Z,C2,0]
Type: List(Homology) |
Klein bottle example
[Z,Z+C2,0] |
(21) -> kbD := kleinBottle()$DCF
(21)
2D:[[1,2,1,- 2]]
1D:[[1,- 1],[1,- 1]]
0D:[[0]]
Type: DeltaComplex(Integer)
(22) -> kbS := kleinBottle()$SCF
(22) points 1..8
(3,4,8)
(2,3,4)
(2,4,6)
(2,6,8)
(2,5,8)
(3,5,7)
(2,3,7)
(1,2,7)
(1,2,5)
(1,3,5)
(4,5,8)
(4,5,7)
(4,6,7)
(1,6,7)
(1,3,6)
(3,6,8)
Type: FiniteSimplicialComplex(Integer)
(23) -> homology(kbD)
(23) [Z,Z+C2,0]
Type: List(Homology)
(24) -> homology(kbS)
(24) [Z,Z+C2,0]
Type: List(Homology) |