Maths - Functor Category

	In a functor category the object is a functor.
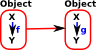	Morphisms are structure preserving maps between these functors.

Since the objects are all functors from X to Y we can redraw it like this:

So we can the that these morphisms are really natural transformations (as described on page here).

So a functor category is a category where:

• The objects are functors.
• The morphisms are natural transformations.

Example of a Functor Category

See presheaves on page here.

Endofunctor Category

In addition to the stucture in the endofunctor we also get structure because endofunctors compose.

This gives a monoidal category where the binary operation is the composition of the endofunctors and the unit is the Id functor.

• The binary operation is a tensor product.
• The unit is the Id functor.

What are the initial and terminal objects in this category?

Is the teminal object the Id functor? (this thread says no).

Pointed Endofunctor

It is well pointed if: S σ = σ S

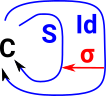Monoidal Category

The above endofunctor category is a monoidal category.

• see page here for tensor product in Graph
• see page here for matrix tensor product.

 

 

Related Categories

• Arrow Category

 

 

 

 

 

 

 

 

 

 

 

 

 

 

EuclideanSpace

home

Prerequisites

• Exponents see the page here.
• Hom Sets see the page here.

Related Subjects

• Fibres

Endofunction

Polynomial Endofunctor