At the moment there is not an '+' function to do superposition, I think the code needs to updated to provide this but first there need to to be some changes to ensure the facets can be aligned for this to work properly.
Here I have tried to illustrate the situation with a very simple example. If we have one edge from a point and we want to add it to a different edge from the same point. The chain complexes are shown on the right. Note how the matricies can be added to give the correct result but only if they are padded out with zeroes to leave space for the other points and lines. |
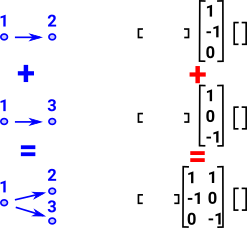 |
We want to add two chain complexes together in a linear way to give a new chain complex. This is provided that we are sure the indexes are aligned properly. The easiest way to do this would be to have a preexisting framework of points, lines, etc. At the start they can all have zero multipliers to indicate empty space, then we can add facets in a linear way.
- Where the topology is represented by a simplicial complex this is relatively simple since everything is mapped to points we just have to make sure the points are aligned.
- With a delta complex it is more complicated as we need to make sure all the indexes are aligned and we have a mechanism for inserting placeholders for facets that may need to be added later.
- In the case of chain complexes, each corresponding matrix in the chain will be padded out with zeroes to the same dimension so can just be added together.
(1) -> p1:List(List(NNI)) := [[1::NNI,2::NNI]]
(1) [[1, 2]]
Type: List(List(NonNegativeInteger))
(2) -> p2:List(List(NNI)) := [[1::NNI,3::NNI]]
(2) [[1, 3]]
Type: List(List(NonNegativeInteger))
(3) -> p3:List(List(NNI)) := [[1::NNI,2::NNI],[1::NNI,3::NNI]]
(3) [[1, 2], [1, 3]]
Type: List(List(NonNegativeInteger))
(4) -> ASIMP := FiniteSimplicialComplex(Integer)
(4) FiniteSimplicialComplex(Integer)
Type: Type
(5) -> c1 := simplicialComplex([],3,p1)$ASIMP
(5) points 1..3
(1, 2)
Type: FiniteSimplicialComplex(Integer)
(6) -> c2 := simplicialComplex([],3,p2)$ASIMP
(6) points 1..3
(1, 3)
Type: FiniteSimplicialComplex(Integer)
(7) -> c3 := simplicialComplex([],3,p3)$ASIMP
(7) points 1..3
(1, 2)
(1, 3)
Type: FiniteSimplicialComplex(Integer)
(8) -> chain(c1)
+ 1 +
| |
(8) [0 0 0], |- 1|, []
| |
+ 0 +
Type: ChainComplex
(9) -> chain(c2)
+ 1 +
| |
(9) [0 0 0], |- 1|, []
| |
+ 0 +
Type: ChainComplex
(10) -> chain(c3)
+ 1 1 +
| | ++
(10) [0 0 0], |- 1 0 |, ||
| | ++
+ 0 - 1+
Type: ChainComplex
(11) ->
|
chain(c2) seems wrong
((21) -> deltaComplex(c1)$DeltaComplex(Integer)
(21)
1D:[[1, - 2]]
0D:[[0], [0], []]
Type: DeltaComplex(Integer)
20) -> deltaComplex(c2)$DeltaComplex(Integer)
(20)
1D:[[1, - 2]]
0D:[[0], [], [0]]
Type: DeltaComplex(Integer)
|