Translate Delta Complex to Simplicial Complex

 

Examples

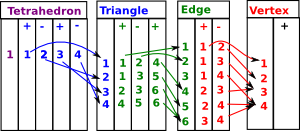
Here is an example of a tetrahedron (2-sphere). indexed table
First we setup 'factories' for DeltaComplex and SimplicialComplex then we convert a SimplicialComplex solid sphere to a DeltaComplex. 
(1) -> DCF := DeltaComplexFactory(Integer)

   (1)  DeltaComplexFactory(Integer)
                                               Type: Type
(2) -> SCF := SimplicialComplexFactory(Integer)

   (2)  SimplicialComplexFactory(Integer)
                                               Type: Type
(3) -> csphere := deltaComplex(sphereSolid(3)$SCF)

   (3)
                          3D:[[1,- 2,3,- 4]]
             2D:[[1,- 2,4],[1,- 3,5],[2,- 3,6],[4,- 5,6]]
         1D:[[1,- 2],[1,- 3],[1,- 4],[2,- 3],[2,- 4],[3,- 4]]
                         0D:[[0],[0],[0],[0]]
                              Type: DeltaComplex(Integer)
(4) -> csphereS := simplicialComplexIfCan(csphere)

   (4)  points 1..4
         (1,2,3,4)
        Type: Union(FiniteSimplicialComplex(Integer),...)

Other Examples

Here we constuct a varoius shapes, using factories created above, first directly as a delta then convert from delta to simplex to compare results.

Unconnected Points

This tests that unconnected points are handled correctly.

This example has 4 points:

  • point 1 and 2 are endpoins of a line.
  • point 3 does not exist but we want to reserve the index.
  • point 4 exist but is not connected to anything.

We want to test that this is correctly converted to a delta complex. 

(5) -> ASIMP := FiniteSimplicialComplex(Integer)

   (5)  FiniteSimplicialComplex(Integer)
                                               Type: Type
(6) -> v1:List(List(NNI)) := [[1::NNI,2::NNI],[4::NNI]]

   (6)  [[1,2],[4]]
                     Type: List(List(NonNegativeInteger))
(7) -> sc1 := deltaComplex(simplicialComplex([],4,v1)$ASIMP)

   (7)
            1D:[[1,- 2]]
         0D:[[0],[0],[],[0]]
                              Type: DeltaComplex(Integer)
(8) -> d1 := simplicialComplexIfCan(sc1)

   (8)  points 1..4
            (4)
           (1,2)
        Type: Union(FiniteSimplicialComplex(Integer),...)

Circle

More about topology of circle on page here.

Constuct a circle first directly as a delta then convert from simplex.

The first delta representation is much simpler as it allows us to use only one point. 

(9) -> cD := circle()$DCF

   (9)
         1D:[[1,- 1]]
           0D:[[0]]
                              Type: DeltaComplex(Integer)
(10) -> cS2 := sphereSurface(2)$SCF

   (10)  points 1..3
            (1,2)
           -(1,3)
            (2,3)
                   Type: FiniteSimplicialComplex(Integer)
(11) -> cD2 := deltaComplex(cS2)

   (11)
          1D:[[1,- 2],[- 1,3],[2,- 3]]
                0D:[[0],[0],[0]]
                              Type: DeltaComplex(Integer)
(12) -> cS := simplicialComplexIfCan(cD)

   (12)  "failed"
                                Type: Union("failed",...)
(13) -> cS3 := simplicialComplexIfCan(cD2)

   (13)  points 1..3
            (1,2)
           -(1,3)
            (2,3)
        Type: Union(FiniteSimplicialComplex(Integer),...)

Dunce Hat

Constuct a dunce hat first directly as a delta then convert from simplex.

Again the first delta representation is much simpler using one point.

 
(14) -> dhD := dunceHat()$DCF

   (14)
          2D:[[1,1,- 1]]
           1D:[[1,- 1]]
             0D:[[0]]
                              Type: DeltaComplex(Integer)
(15) -> dhS2 := dunceHat()$SCF

   (15)  points 1..8
           (1,2,8)
           (2,3,8)
           (3,7,8)
           (1,3,7)
           (1,2,7)
           (1,6,8)
           (1,2,6)
           (6,7,8)
           (2,4,6)
           (5,6,7)
           (2,5,7)
           (4,5,6)
           (2,3,4)
           (2,3,5)
           (1,3,4)
           (1,4,5)
           (1,3,5)
                   Type: FiniteSimplicialComplex(Integer)
(16) -> dhD2 := deltaComplex(dhS2)

   (16)
   VCONCAT
      VCONCAT
         VCONCAT
        ,
             2D:
              [[1,- 5,11], [1,- 6,12], [1,- 7,13],
              [2,- 3,14], [2,- 4,15],
               [2,- 6,16], [3,- 4,18], [5,- 7,23],
               [8,- 9,14], [8,- 10,15],
               [8,- 13,17], [9,- 11,19],
               [10,- 12,21], [16,- 17,24],
               [18,- 19,20], [20,- 21,22], [22,- 23,24]]
     ,
          1D:
           [[1,- 2], [1,- 3], [1,- 4], [1,- 5],
           [1,- 6], [1,- 7], [1,- 8],
            [2,- 3], [2,- 4], [2,- 5], [2,- 6]
            [2,- 7], [2,- 8], [3,- 4],
            [3,- 5], [3,- 7], [3,- 8], [4,- 5]
            [4,- 6], [5,- 6], [5,- 7],
            [6,- 7], [6,- 8], [7,- 8]]
  ,
       0D:[[0],[0],[0],[0],[0],[0],[0],[0]]
                              Type: DeltaComplex(Integer)
(17) -> dhS := simplicialComplexIfCan(dhD)

   (17)  "failed"
                                Type: Union("failed",...)
(18) -> dhS3 := simplicialComplexIfCan(dhD2)

   (18)  points 1..8
           (1,2,6)
           (1,2,7)
           (1,2,8)
           (1,3,4)
           (1,3,5)
           (1,3,7)
           (1,4,5)
           (1,6,8)
           (2,3,4)
           (2,3,5)
           (2,3,8)
           (2,4,6)
           (2,5,7)
           (3,7,8)
           (4,5,6)
           (5,6,7)
           (6,7,8)
        Type: Union(FiniteSimplicialComplex(Integer),...)

Torus Surface

More about topology of torus on page here.

Constuct a torus surface first directly as a delta then convert from simplex to compare results.

Again the first delta representation is much simpler.

 
(19) -> tD := torusSurface()$DCF

   (19)
           2D:[[1,2,- 1,- 2]]
          1D:[[1,- 1],[1,- 1]]
                0D:[[0]]
                               Type: DeltaComplex(Integer)
(20) -> tS2 := torusSurface()$SCF

   (20)  points 1..7
           (1,2,3)
           (2,3,5)
           (2,4,5)
           (2,4,7)
           (1,2,6)
           (2,6,7)
           (3,4,6)
           (3,5,6)
           (3,4,7)
           (1,3,7)
           (1,4,5)
           (1,4,6)
           (5,6,7)
           (1,5,7)
                   Type: FiniteSimplicialComplex(Integer)
(21) -> tD2 := deltaComplex(tS2)

   (21)
   VCONCAT
      VCONCAT
         VCONCAT
        ,
             2D:
              [[1,- 2,7], [1,- 5,10], [2,- 6,15],
              [3,- 4,16], [3,- 5,17],
               [4,- 6,20], [7,- 9,13], [8,- 9,16],
                [8,- 11,18], [10,- 11,21],
               [12,- 14,17], [12,- 15,18],
               [13,- 14,19], [19,- 20,21]]
     ,
          1D:
           [[1,- 2], [1,- 3], [1,- 4], [1,- 5],
           [1,- 6], [1,- 7], [2,- 3],
            [2,- 4], [2,- 5], [2,- 6], [2,- 7],
            [3,- 4], [3,- 5], [3,- 6],
            [3,- 7], [4,- 5], [4,- 6], [4,- 7],
            [5,- 6], [5,- 7], [6,- 7]]
  ,
       0D:[[0],[0],[0],[0],[0],[0],[0]]
                              Type: DeltaComplex(Integer)
(22) -> tS := simplicialComplexIfCan(tD)

   (22)  "failed"
                                Type: Union("failed",...)
(23) -> tS3 := simplicialComplexIfCan(tD2)

   (23)  points 1..7
           (1,2,3)
           (1,2,6)
           (1,3,7)
           (1,4,5)
           (1,4,6)
           (1,5,7)
           (2,3,5)
           (2,4,5)
           (2,4,7)
           (2,6,7)
           (3,4,6)
           (3,4,7)
           (3,5,6)
           (5,6,7)
        Type: Union(FiniteSimplicialComplex(Integer),...)

Projective Plane

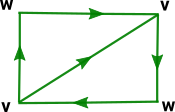
That is, a real projective space in 2 dimensions (ℜP²).

More about topology of projective plane on page here.

real projective
Constuct a projective plane first directly as a delta then convert from simplex to compare results. 
(24) -> ppD := projectiveSpace(2)$DCF

   (24)
           2D:[[1,1]]
          1D:[[1,- 1]]
            0D:[[0]]
                               Type: DeltaComplex(Integer)
(25) -> ppS2 := projectiveSpace(2)$SCF

   (25)  points 1..6
           (1,2,3)
           (1,3,4)
           (1,2,6)
           (1,5,6)
           (1,4,5)
           (2,3,5)
           (2,4,5)
           (2,4,6)
           (3,4,6)
           (3,5,6)
                   Type: FiniteSimplicialComplex(Integer)
(26) -> ppD2 := deltaComplex(ppS2)

   (26)
   VCONCAT
      VCONCAT
         VCONCAT
        ,
             2D:
              [[1,- 2,6], [1,- 5,9], [2,- 3,10],
              [3,- 4,13], [4,- 5,15],
               [6,- 8,11], [7,- 8,13], [7,- 9,14],
               [10,- 12,14], [11,- 12,15]]
     ,
          1D:
           [[1,- 2], [1,- 3], [1,- 4], [1,- 5],
           [1,- 6], [2,- 3], [2,- 4],
            [2,- 5], [2,- 6], [3,- 4], [3,- 5],
            [3,- 6], [4,- 5], [4,- 6],[5,- 6]]
  ,
       0D:[[0],[0],[0],[0],[0],[0]]
                              Type: DeltaComplex(Integer)
(27) -> ppS := simplicialComplexIfCan(ppD)

   (27)  "failed"
                                Type: Union("failed",...)
(28) -> ppS3 := simplicialComplexIfCan(ppD2)

   (28)  points 1..6
           (1,2,3)
           (1,2,6)
           (1,3,4)
           (1,4,5)
           (1,5,6)
           (2,3,5)
           (2,4,5)
           (2,4,6)
           (3,4,6)
           (3,5,6)
        Type: Union(FiniteSimplicialComplex(Integer),...)

Klein Bottle

Constuct a Klein bottle first directly as a delta then convert from simplex to compare results. 
(29) -> kbD := kleinBottle()$DCF

   (29)
            2D:[[1,2,1,- 2]]
          1D:[[1,- 1],[1,- 1]]
                0D:[[0]]
                              Type: DeltaComplex(Integer)
(30) -> kbS2 := kleinBottle()$SCF

   (30)  points 1..8
           (3,4,8)
           (2,3,4)
           (2,4,6)
           (2,6,8)
           (2,5,8)
           (3,5,7)
           (2,3,7)
           (1,2,7)
           (1,2,5)
           (1,3,5)
           (4,5,8)
           (4,5,7)
           (4,6,7)
           (1,6,7)
           (1,3,6)
           (3,6,8)
                   Type: FiniteSimplicialComplex(Integer)
(31) -> kbD2 := deltaComplex(kbS2)

   (31)
   VCONCAT
      VCONCAT
         VCONCAT
        ,
             2D:
              [[1,- 3,8], [1,- 5,10], [2,- 3,13],
              [2,- 4,14], [4,- 5,23],
               [6,- 7,12], [6,- 10,15], [7,- 9,18],
                [8,- 11,22], [9,- 11,24],
               [12,- 16,20], [13,- 15,21],
               [14,- 16,24], [17,- 19,21],
               [17,- 20,22], [18,- 19,23]]
     ,
          1D:
           [[1,- 2], [1,- 3], [1,- 5], [1,- 6],
           [1,- 7], [2,- 3], [2,- 4],
            [2,- 5], [2,- 6], [2,- 7], [2,- 8],
            [3,- 4], [3,- 5], [3,- 6],
            [3,- 7], [3,- 8], [4,- 5], [4,- 6],
            [4,- 7], [4,- 8], [5,- 7],
            [5,- 8], [6,- 7], [6,- 8]]
  ,
       0D:[[0],[0],[0],[0],[0],[0],[0],[0]]
                              Type: DeltaComplex(Integer)
(32) -> kbS := simplicialComplexIfCan(kbD)

   (32)  "failed"
                                Type: Union("failed",...)
(33) -> kbS3 := simplicialComplexIfCan(kbD2)

   (33)  points 1..8
           (1,2,5)
           (1,2,7)
           (1,3,5)
           (1,3,6)
           (1,6,7)
           (2,3,4)
           (2,3,7)
           (2,4,6)
           (2,5,8)
           (2,6,8)
           (3,4,8)
           (3,5,7)
           (3,6,8)
           (4,5,7)
           (4,5,8)
           (4,6,7)
         Type: Union(FiniteSimplicialComplex(Integer),...)
metadata block
see also:
Correspondence about this page

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.