We can represent a torus as a delta complex like this: That is: there is one vertex 'x' and two independent loops on it. |
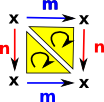 |
| To avoid having multiple copies of the vertex 'x' we can embed it in 3 dimensions, then first wrap the loop 'n' back to itself: |  |
| We can then loop this whole loop back to itself: |
In the program FriCAS (described here) there is a function: torusSurface which generates a minimal triangulation of the surface of an 3-dimensional torus.
Torus - (1) -> torusSurface()
+1 2 3+
|2 3 5|
|2 4 5|
|2 4 7|
|1 2 6|
|2 6 7|
(1) |3 4 6|
|3 5 6|
|3 4 7|
|1 3 7|
|1 4 5|
|1 4 6|
|5 6 7|
+1 5 7+
Type: FiniteSimplicialComplex(VertexSetAbstract)
|
No boundaries, the red arrows at the top and bottom join up and the blue arrows on the left and right join up. 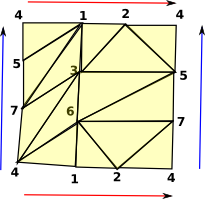 |