Maths - Category Theory - Adjunction

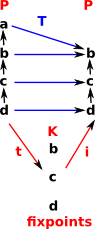
This page describes some examples of adjunctions. Adjunctions were introduced on the page here.

Example - Monoid

On this page is an example of an adjunction between set and a free monoid (List monad).

Example - Preordered Set

See this page for preordered set example.

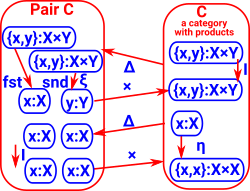
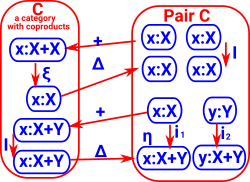
Sum and Product

+Δ×

The top triangle is the co-unit:
ξ : Δ • × -> I

The lower triangle is the unit:
η : I -> × • Δ

The top triangle is the co-unit:
ξ : + • Δ -> I

The lower triangle is the unit:
η : I -> Δ • +

This is explained by Bartosz Milewski on his blog here.

We can also relate this to logic:

existential,sum Σ		weakening (adding an extra assumption)
weakening		universal, product Π

Currying

This relates product to functions.

Some Other Very General Adjunctions


equality		contraction
truth		comprehension or subset types
equality		comprehension
quotients		equality

Adjoint Pairs

The basis on a vector space

The free group on a set

G G / [G,G] commutator subgroup

universal enveloping algebra of a Lie algebra

completion of a metric space

Category of Graphs

described on page here.

Between reflexive graph and set.

In reflexive graph: every node has loop to itself.

graph example

irreflexive

Between irreflexive graph and set.

In irreflexive graph: every node does not have loop to itself.

Between dynamical system graph and set.

In dynamical system graph: every node has one outgoing arrow.

Different dynamical system graph and set.

This time the morphism to set defines the fixpoints.

Poset

An endofunctor on posets models closure. Posets don't have loops, therefore defined by fixpoints.

Define T: P -> P

with

x <= T x
T² x <= T x

gives

T² <= T (that is it is idempotent)

Which gives an adjunction: ti

This is discussed as a monad on page here.

Implementing Posets in FriCas program is discussed on page here.

Category
type theory	quantifiers	substitution (Cartesian maps)

References

Conceptual Mathematics - This is a book about category theory that does not assume an extensive knowledge over a wide area of mathematics. The style of the book is a bit quirky though.

Implementing Graphs in FriCas program is discussed on page here.

EuclideanSpace

home

Prerequisites

We need to know about category theory concepts described on these pages and, in particular, natural transformations.

Ø	empty set
¬	not
∧	and (= intersection)
∨	or (U = union)
	is in (is an element of the set)
==>	if
<=>	if and only if (iff)
	for all
	there exists (for some)
	is isomorphic to

Maths - Examples of Adjunctions