I am looking for the simplest example of an adjunction that I can find so lets try to find an adjunction in sets. I haven't seen such an example in the literature so it may be that this is impossible.
As with other examples here, these diagrams look inside the objects and morphisms, this is not really a category theory approach but is intended to help intuition when relating to other approaches.
| Lets take a surjective mapping from the set C to the set D: | 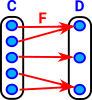 |
We can't reverse the surjective mapping exactly so what's the nearest we can get? One possibility is, where multiple arrows come from different elements, is just to choose one element for the reverse mapping. However having to make an arbitary choise of elements dosent seem a ver category theory approach. So here I have mapped back to a set of sets, where the inner sets are equivilance classes of all the elements that map to each element in D. See fibre bundle on page here. |
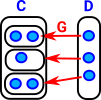 |
| Here I have tried to draw the natural transformations at each end. | 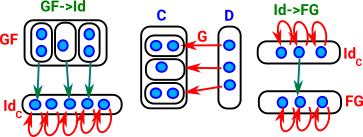 |