Maths - Category Theory - Adjunctions

Example - Monoid

'term' or 'word' algebras determines an adjunction

This example looks at extremes such as the forgetful functor in one direction (which removes all structure and leaves the underlying set) and the free algebra in the other direction (see Presentation of a group. Free algebra has generators without constraints).

Free Monoid

Here we have a set {a,b,c...} with a binary operation. When we apply the binary operation to two elements of the set, say a × b, we get a new element which we could notate as 'ab'.

List

Another way to think of this free monoid is by representing a × b = [a,b]

So this list is an element of the free monoid. The function which takes a list 'T A' to the new element 'A' is called θ:

θ : T A -> A

Here think of 'T' as a generic notation for 'List'.

Functors between Set and Monoid

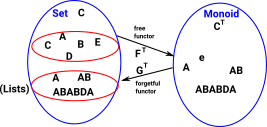
So,

• G is the forgetful functor which goes from monoid to set and removes the structure (multiplication and identity) and,
• F goes from set to monoid and creates a free monoid, since there are no relations, the elements of the set don't interact and remain as a word or list.

therefore:

• μ : 1_monoid => FG is a transformation within monoid, which forgets the existing structure and creates a free structure.
• ξ : GF => 1_set is a transformation within set, which creates a free monoid (list) and then forgets the structure to return the elements of the set.

Forgetful functor from monoid to set. Takes the algebra and returns the underlying set
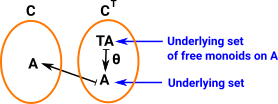Free functor from set to monoid. Takes the underlying set and returns a monoid with a multiplication.

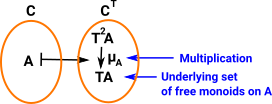Adjunction to Monad

So we have two functors 'F' and 'G'. If we start with set and apply the free functor 'F' first and then the forgetful functor 'G' which we denote as 'GF' we get a set containing all possible lists of elements which is 'T'.

Monad to Adjunction

The final and initial adjunctions from 'T' are given by the base category (in this case set) with the monoid which can be generated in the following ways:

Eilenberg-Moore Category for Monoid

This is final in the categories for the monad.

• The objects are θ : T A -> A
• The morphisms are the same as the underlying set: A->B.

So we just 'freely' apply θ to the elements of the underlying set to produce the elements of the monoid.

Kleisli Category for Monoid

This is initial in the categories for the monad.

• The objects are the same as the underlying set: A.
• The morphisms are: A -> T B.

In other words the morphisms wrap the elements in a list: A -> List B.

This makes function composition more complicated. When we compose

A -> List B

with B -> List C

we get

A -> List (List C)

but we want:

A -> List C

So we have to apply μ to get from List (List C) to List C.

In this case μ just flattens the nested list to produce one list with all the elements.

EuclideanSpace

home

Prerequisites

We need to know about category theory concepts described on these pages and, in particular, natural transformations.