This page continues our discussion of finite and permutation groups from this page. Here we look at how to define and categorise the groups in a more formal way.
Ways to define the structure of a group
What is the minimum information required to define the structure of this group? We could:
- Specify each permutation in the group by using the arrows (as shown in the triangle example) for each permutation.
- Specify each permutation in the group by using the cycle notation for each permutation.
- Use the Cayley table for the group.
But is there any other way?
Presentation of a group
It turns out that we can specify the group by its generators plus a set of relations among the generators (relations that produce the identity element are usually written without the equals sign).
This is known as the 'Presentation of a group'.We specify this as follows:
Γ< generators | relations >
Using the triangle example, from this page, we have:
Γ< a,b | aa,bb,bab=aba>
We could have set all relations to be equal to unity by replacing bab=aba with baba-1b-1a-1=1
Can we use this to generate all the entries in the table and thus completely define the structure?
Lets take an example of multiplying 'ab' by 'ab':
ab * ab = abab [associatively]
= aaba [since bab=aba]
= ba [since aa=1]
Doing this for all the other entries in the Cayley table shows that this completely defines the group. How can we work out the minimum set of relations that will define the group?
Cayley Graph
This shows all the group elements as points with arrows (colour coded) for each
Free Group
This is a group whose presentation has no relations. This means that it is an infinite group (although finitely generated) because each time the generators are applied they will generate new elements of the group. So the relations have the effect of reducing the number of possible elements
Group Examples
So a free group (which nas no relations) is infinite because, each time we apply a generator, a new element is produced. So, in the table below, I have started adding relations to see how many we need to add to make the group finite.
I first added one relation (a²=1), this prevents a sequence of 'a's but we can still have a potentially infinite sequence of 'b's or an alternating 'ababa…' sequence.
I then added (b²=1), but this still allows a potentially infinite alternating sequence 'ababa…'.
It was only when I added a third relation that the group became finite.
| Presentation | Cayley graph | |
|---|---|---|
| Free Group | Γ = < a,b… | Ø> | 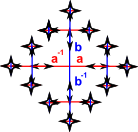 |
| One relation | Γ = < a,b | a² > | 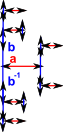 |
| Two relations | Γ = < a,b | a²,b² > |  |
| Γ = < a,b | a²,b²,ab=ba > | 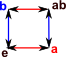 |
|
Dihedral Group (rotation and reflection of a triangle) see this page for full description. |
D3= < a,b | aa,bb,bab=aba> or D3= < a,b | aa,bbb,a-1ba=b-1> |
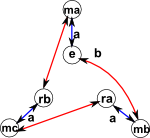 |
| Cube (see this page) |  |
|
| complex number | C = < a,b | a²=b,b²,ab=ba> | I'm not sure if this is minimum representation (this represents a=i, b=-1) |
| quaternion | H = <a,b | a² = b² = (ab)²> or H = < a,b | a 4,a²=b²,b-1ab=a-1> |
|
| Two dimensional Clifford algebra (see this page) | Γ= < a,b,-e,-a,-b | a²,b²,(-a)²,(-b)²,(-e)²,a(-a)=-e,b(-b)=-e,ab=-ba > | 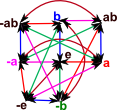 |
