here the group elements of the resulting group are sets containing an element from each on the multiplicands.
Example 1
Lets take the simplest example we can think of. Lets take the group Z2 which is the integers modulo two which gives an exclusive or table:
Cayley Table |
Cayley Graph |
|||||||||
|
Lets combine two of these groups to give: Z2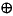 Z2
Z2
{g, h} × {g' , h' } = {g * g' , h o h' }
where:
- × is the operation of the combined algebra.
- * is the operation of the group G.
- o is the operation of the group H which may be, or may not be, the same as *.
Cayley Table |
|
|||||||||||||||||||||||||
| Cayley Graph |  |
Is there any way we can modify this to generate the complex numbers?
Can we then go on to generate the quaternions and octonions?
- H = C
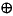 C
C - O = H
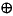 H
H