This is a modification to the direct product described on this page. Here we will apply a mapping to one of the operands before applying the direct product:
{n, h}![]() φ {n',h'} = {n * φ(n') , h o h' }
φ {n',h'} = {n * φ(n') , h o h' }
where:
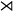 is the operation of the combined algebra (right handed semidirect product).
is the operation of the combined algebra (right handed semidirect product).- * is the operation of the group G.
- o is the operation of the group H which may be, or may not be, the same as *.
- φ() is a mapping as described below.
Here we are using the right handed semidirect product ![]() , we can change to the left handed semidirect product
, we can change to the left handed semidirect product![]() by exchanging the operands.
by exchanging the operands.
The mapping is done as follows, we first generate cosets of the first group, we apply the group operation to these cosets but slightly modified as follows:
- If we are thinking in terms of the Cayley graph then we reverse the arrows of all permutations of the generators.
- If we are thinking in terms of the Cayley table then we swap rows with their inverse.
We then use a mapping of the second group to select which coset to use for each product of the second group.
Example C2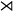 C3
C3
As with the direct product example we will try calculating the product of C2 and C3. As a reminder these are the definitions of these groups individually (full definitions on this page):
C2
| generator | cayley graph | table | permutation | representation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <m | m²> |
|
< ( 1 2 ) > |
|
C3
| generator | cayley graph | table | permutation | representation | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <r | r³> |  |
|
< ( 1 2 3 ) > |
|
direct product C3 × C2
This gives :
| generator | cayley graph | table | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <m,r | m²,r³,rm=mr> |  |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| permutation | representation | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| <(1 2 3)(4 5 6),(1 4)(2 5)(3 6)> |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Note that, in addition to applying both the generators and constrains for the original groups we have had to apply an additional constraint: rm=mr. If we had not done this we would have the infinite free product.
Generating a Semidirect Product using a Program
We can use a computer program to generate these groups, here I have used Axiom/FriCAS which is described here.
(1) -> )r axiom/semidirectProduct
)set output algebra off
)set output mathml on
-- first try C2 x C3
C2 := FiniteGroup(2,[[1,2],[2,1]],["1","m"])
Type: Type
SDP := semidirectProduct([[1,2,3],[2,3,1],[3,1,2]],["1","r","rr"],
[[2,2,2],[2,2,2],[2,2,2]])$C2
Type: Type
toTable()$SDP
Type: Table(6)
setGenerators([false,true,false,true,false,false])$SDP
Type: Void
PSDP := toPermutation()$SDP
<(1 2 3)(4 5 6),(1 4)(2 5)(3 6)>
Type: PermutationGroup(Integer)
permutationRepresentation(PSDP,6)
Type: List(Matrix(Integer))
-- then try C3 x C2 with mapping [[2,2],[2,2]]
C3 := FiniteGroup(3,[[1,2,3],[2,3,1],[3,1,2]],["1","r","rr"])
Type: Type
SDP := semidirectProduct([[1,2],[2,1]],["1","m"],[[2,2],[2,2]])$C3
Type: Type
toTable()$SDP
Type: Table(6)
setGenerators([false,true,true,false,false,false])$SDP
Type: Void
PSDP := toPermutation()$SDP
<(1 2)(3 4)(5 6),(1 3 5)(2 4 6)>
Type: PermutationGroup(Integer)
permutationRepresentation(PSDP,6)
Type: List(Matrix(Integer))
-- then try C3 x C2 with mapping [[1,1],[2,2]]
C3b := FiniteGroup(3,[[1,2,3],[2,3,1],[3,1,2]],["1","r","rr"])
Type: Type
SDP := semidirectProduct([[1,2],[2,1]],["1","m"],[[1,1],[2,2]])$C3b
Type: Type
toTable()$SDP
Type: Table(6)
setGenerators([false,true,true,false,false,false])$SDP
Type: Void
PSDP := toPermutation()$SDP
<(1 2)(3 6)(4 5),(1 3 5)(2 4 6)>
Type: PermutationGroup(Integer)
permutationRepresentation(PSDP,6)
Type: List(Matrix(Integer))
(19) ->
|
Examples
Here are some examples of the semidirect product of groups:
| Type | Product | Description |
|---|---|---|
| Dihedral Group |
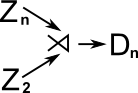 |
The dihedral group is the semidirect product of a cyclic group of order 2 and a cyclic group of order n |
| Isometries | 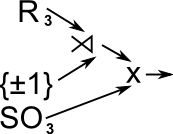 |
Isometries (distance preseving maps) in 3-space is the semidirect product of:
|
| Poncaré |  |
Poncaré group is the semidirect product of:
|