An inductive definition of a type is given by a list of constructors. Each of these constructors has a signature like the following examples:
| name : T | no parameters defines a single term (element) of the type |
| name: Nat -> T | defines a term for every term of Nat |
| name: Nat -> Nat -> T | defines a term for every pair of Nats |
| name: T -> T | defines a potentially infinite sequence of terms |
| name: T -> T -> T | defines a potentially infinitely deep tree of terms |
| name: (Nat -> T) -> Nat -> T | covariant terms like (Nat -> T) can appear as parameters but not contravariant terms like (T -> Nat). |
So:
- The type being defined can appear as an input to a constructor but only strictly positively (covariant not contravariant).
- If we want an infinite number of constructors we use a term like Nat -> (T -> T).
- If we want an infinite number of parameters we use a term like (Nat -> T) -> T.
As an example we might have these 3 constructors:
- (A -> T) -> T
- (B -> C -> T) -> T
- D -> T -> T
These can be combined into a single constructor:
c : (A -> T) -> (B -> C -> T) -> D -> T -> T
Recursion Principle
This is the eliminator for non-dependant types.
In order to construct a property P (which is a type, such as an equation) from our type T. That is a function f of type:
f : T -> P:Type
it suffices to consider the case where the input t:T arises from one of the constructors, allowing ourselves to recursivly call f on the inputs to that constructor.
So for the example given above:
- (A -> T) -> T
- (B -> C -> T) -> T
- D -> T -> T
- A -> P
- B -> C -> P
- D -> T -> P
Bringing this together we would require P to be equipped with a function of type:
d : (A -> T) -> (A -> P) -> (B -> C -> T) -> (B -> C -> P) -> D -> T -> P -> P.
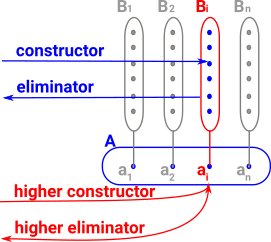
Constructors for Higher Types
For dependent types we can now have multiple levels of constructors.
- The ordinary constructors we have discussed so far, known as point constructors.
- Higher level constructors, known as path constructors.
 |
Idris Code Examples
An example of a 'point' constructor is Nat. So we are just constructing a simple type so the constructors have this form: Z -> Nat which are of type: F(T) -> T where 'T' is a type being constructed |
||| Natural numbers: unbounded, unsigned ||| integers which can be pattern matched. data Nat = ||| Zero Z | ||| Successor S Nat |
Whereas to construct a 'path' type we have constructors of the form: F(a->T) -> (a->T) where 'T' is a type and 'a' is a term of some type. Here we are constructing the path: a->T |
|| Vectors: Generic lists with explicit length in the type ||| @ len the length of the list ||| @ elem the type of elements data Vect : (len : Nat) -> (elem : Type) -> Type where ||| Empty vector Nil : Vect Z elem ||| A non-empty vector of length `S len`, consisting of ||| a head element and the rest of the list, of length `len`. (::) : (x : elem) -> (xs : Vect len elem) -> Vect (S len) elem |
For example to construct a vector, such as [1,2,3], we first have to construct a type of vectors of size 3 then we can construct an element of this type. Some programs will do the higher construct automatically without the need for an explicit command.
Induction Principle
This is the eliminator for dependant types.