On their own, sets don't have much structure. Often when talking about 'sets' we mean sets with functions between them. For instance, in category theory, the category of sets (discussed on this page) gets its structure from the arrows.
To keep things simple on this page we are mostly talking about 'total' functions as opposed to 'partial' functions and we are looking at finite functions. Also here we will use the terms 'functions' and 'maps' interchangeably.
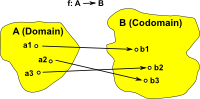
| For a finite function we can 'look inside' it, that is, draw a diagram showing which element in the co-domain is mapped to by each element in the domain. |  |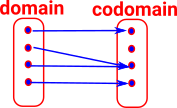
 |
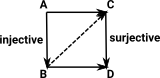This type of function can be factorised into a pair of functions one injective and the other one surjective. (see 'weak factorisation system on this page) |
The meaning of injective and surjective is as follows:
Injective, Surjective and Bijective Functions
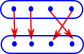
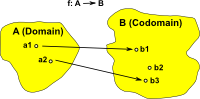
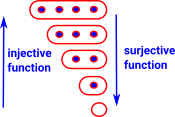
Injective function Every element in the domain is mapped to a unique element in the codomain. There may be elements in the domain that are not used. (size of domain <= size of codomain) |
 |
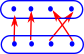
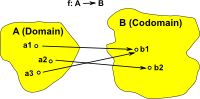
Surjective (onto) Elements in the domain may be mapped to the same element in the codomain but every element in the codomain is targeted. (size of domain >= size of codomain) |
 |
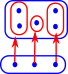
Bijective function Every element in the domain is mapped to a unique element in the codomain and every element in the codomain is mapped to a unique element in the domain. (size of domain = size of codomain) |
 |
Graded Structure
We can get more structure just from sets and the functions between them. In the category of sets the objects are sets with 'n' elements, without any lables for the elements all sets of the same size are the same. This gives us the natural number structure. Bijective functions do not change the number of elements, otherwise: Injective functions increase the number of elements. Surjective functions decrease the number of elements. |
 |
 |
If we label the elements we can see more structure. The injective functions can be factored into a sequence of injective functions each of which increments the number of elements by 1. The surjective functions can be factored into a sequence of surjective operations each of which decrements the number of elements by 1. |
So we can represent any function by a sequence of increments or decrements. Each increment would require one parameter containing the element number to be inserted and each decrement would require two parameters containing the element numbers to be merged.
Setop
The structure discussed so far is not symmetrical in that, if we reverse a function, the result may not be another function. In category theory not every arrow has to be a function.
When we reverse the arrows in set then we get the opposite of a function as follows:
| There may be multiple arrows out of each element. | |
| There may be no arrows out of each element. | |
| There cannot be no arrows in to each element. |  |
| There cannot be multiple arrows in to each element. |  |
This page discusses setop in the context of category theory.
Where there are two arrows coming out of an element we can look at this as generating 'degenerate elements' that is the two elements are considered the same as each other.
Setoid Structure
A setoid structure is a set structure with a separate equivalence relation imposed on it from outside (as explained on page here).
We could look as the equivalent elements as being the 'degenerate elements' discussed above thereby relating these concepts.
Simplicial Sets
If we constrain the functions, discussed on this page, to be (weakly) order preserving inverse-functions then we have a simplicial set structure as described on the page here.
Set + Structure
In its purest form the only information contained in a set is the number of elements it contains. All other information, such as labeling the elements, can be added using functions between sets.
A total function maps every element in the domain to an element in the codomain. Although not every element in the codomain may necessarily be mapped too. So, in this way functions between sets are not necessarily symmetrical.
From this mathematical structure is genererated.
Bijective functions are invertible. See: |
 |
 |
Surjective functions are not invertible in that we can't reverse the function and get back to where we started, for instance if we have a surjective mapping from set to set we can't get back to the same set, however we can go back to a 'set of sets'. This gives rise to interesting structure, see: |
|
 |
Injective functions gives a subobject structure. If we have an injective mapping from set to set we can't get back to the same set, however we can have a mapping from set to Bool which tells us which element are in the subset, this is known as a characteristic function in sets or 'subobject classifier' more generally in category theory. This subobject structure is interesting see:
|
|
 |
This page explains bijection, injection and surjection.
Further Development
Further development of this subject on these pages:
