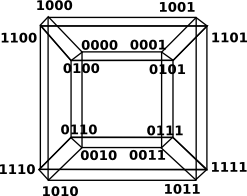
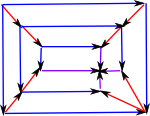
As an alternative to simplicial complexes we can base our topology on squares rather than triangles.
Examples of Complexes
Solid Sphere - In this case 2 dimentional square: (1) -> sp :=
sphereSolid(2)$CubicalComplexFactory
(1)
(1..2,1..2)
Type: FiniteCubicalComplex(Integer)
|
|
Sphere Surface - In this case 2 dimentional square sides: (2) -> sps :=
sphereSurface(2)$CubicalComplexFactory
(2)
-(1..1,1..2)
(2..2,1..2)
(1..2,1..1)
-(1..2,2..2)
Type: FiniteCubicalComplex(Integer) |
|
Band - Cylinder without ends: (3) -> bnd := band()$CubicalComplexFactory
(3)
(1..1,1..2,1..2)
(2..2,1..2,1..2)
(1..2,1..1,1..2)
(1..2,2..2,1..2)
Type: FiniteCubicalComplex(Integer) |
|
Torus - (4) ->tor := torusSurface()$CubicalComplexFactory
(4)
(1..1,1..2,1..1,1..2)
(1..1,1..2,2..2,1..2)
(1..1,1..2,1..2,1..1)
(1..1,1..2,1..2,2..2)
(2..2,1..2,1..1,1..2)
(2..2,1..2,2..2,1..2)
(2..2,1..2,1..2,1..1)
(2..2,1..2,1..2,2..2)
(1..2,1..1,1..1,1..2)
(1..2,1..1,2..2,1..2)
(1..2,1..1,1..2,1..1)
(1..2,1..1,1..2,2..2)
(1..2,2..2,1..1,1..2)
(1..2,2..2,2..2,1..2)
(1..2,2..2,1..2,1..1)
(1..2,2..2,1..2,2..2)
Type: FiniteCubicalComplex(Integer) |
|
Möbius band: One boundary: not yet implemented |
|
Projective Plane - No boundaries, every edge is connected to two faces: (6) -> pp :=
projectiveSpace(2)$CubicalComplexFactory
(5)
(1..2,1..1,1..1,1..2,1..1)
(1..2,1..1,1..1,1..1,1..2)
(1..1,1..2,1..2,1..1,1..1)
(1..1,1..2,1..1,1..2,1..1)
(1..1,1..1,1..2,1..1,1..2)
(1..2,1..2,2..2,1..1,1..1)
(1..2,2..2,1..2,1..1,1..1)
(2..2,1..2,1..2,1..1,1..1)
(1..2,1..2,1..1,1..1,2..2)
(1..2,2..2,1..1,1..1,1..2)
(2..2,1..2,1..1,1..1,1..2)
(1..2,1..1,1..2,2..2,1..1)
(1..2,1..1,2..2,1..2,1..1)
(2..2,1..1,1..2,1..2,1..1)
(1..1,1..2,1..1,1..2,2..2)
(1..1,1..2,1..1,2..2,1..2)
(1..1,2..2,1..1,1..2,1..2)
(1..1,1..1,1..2,1..2,2..2)
(1..1,1..1,1..2,2..2,1..2)
(1..1,1..1,2..2,1..2,1..2)
Type: FiniteCubicalComplex(Integer) |
|
Further Information
For corresponding factory for simpectial complexes see page here.
For more general information about cubical complexes see page here .
My code for this page is on github here.