Physics - Inverse Kinematics (IK)

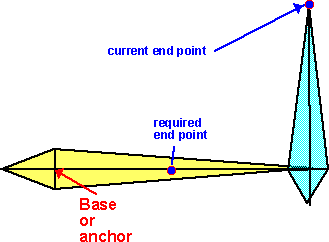
For inverse kinematics (IK), the position of the end point is known, and we need to find the angles of the joints. This is a much harder problem, there may be many possible answers, or there may not be a set of angles that would reach to that point. Although this is hard to do, it is useful, for example, when posing a model it is useful to be able to drag the extremities with a mouse and have the arms/links position themselves appropriately.

There are two approaches to solving inverse kinematics:

• Analytical - requires a lot of trigonometry or matrix algebra
• Iterative - better if there are lots of links and degrees of freedom.

IK - Analytical approach

If there are only two or three links then it may be possible to solve it analytically. One possibly might be to draw out the arm with the angles shown on it, then solve for the angles using geometry, a good knowledge of trig identities would help here. The problem is that this is not really very general approach.

Another analytical approach is to represent each links rotation and translation by a matrix. The end point is then given by all these matrixes multiplied together, so we just need to solve this matrix equation. Then find what rotation each matrix represents.

There may be many solutions or there may not be any solutions. In other words there are lots of ways to reach to a given point, or it may be out of reach.

If there are many solutions, then you might need to apply additional constraints. For instance, human joints can only bend within certain limits.

IK - Iterative approach

This is a more general approach for programming complex chains.

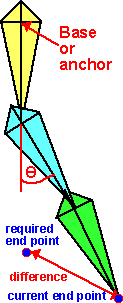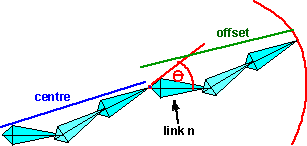
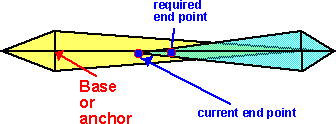
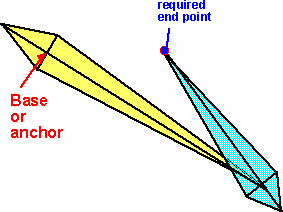
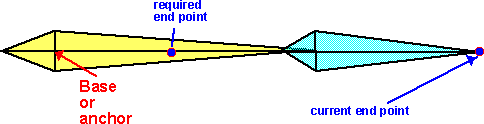
Start off with the joints in any position, then move each of the joints in turn, so that each movement takes the endpoint toward the target. Starting with the joint nearest the end point, rotate the joint so that the current end point moves toward the required end point. Then do the same with the next joint toward the base and so on until the base is rotated. Then keep repeating this, until the end point is close enough to the required end point or if further iterations are not moving it closer to the required point. It may be possible to have a more realistic strategy than this, for instance, if I am using my arm to pick up an object then, if the object is a long way away, I will move the bigger joints in the arm, then as the hand gets closer the smaller joints of the hand are used for the fine adjustments. The angle of rotation for each joint is found by taking the dot product of the vectors from the joint to the current point and from the joint to the desired end point. Then taking the arccos of this dot product. To find the sign of this angle (ie which direction to turn), take the cross product of these vectors and checking the sign of the Z element of the vector.

For more information about calculating the angle to turn see the lookAt function here.

Data Structure

We can store the relative positions and orientations of the links in a scenegraph as described in the forward kinematics page.

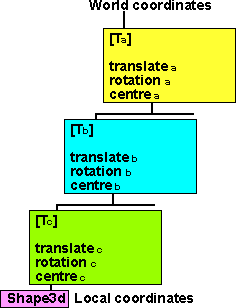
For a more detailed suggestion of how to store this information see these pages. These pages suggest how we can specify constraints to make different types of joints.

Code

So from the iterative approach above the algorithm for an n-link chain is:

sfvec3f translation[n]; // translation for each link
sfrotation rotation[n]; // rotation for each link
sfvec3f centre[n]; // centre of rotation for each link
while (distance < lastDistance) {
	for (int link=0,link<n,link++) {
		translation[link] = calculateOffsetForThisLink();
		rotation[link] = calculateRotationForThisLink();
		centre[link] = calculateCentreForThisLink();
        lookAt(translation[link],rotation[link],centre[link]);
	}
}

where:

• lookAt = is defined here
• can anyone help me define these functions: calculateOffsetForThisLink(), calculateRotationForThisLink(), calculateCentreForThisLink()

Convergence

Does this method always converge?

Sometimes there seem to be local minima such that changing one angle at a time does not move us closer to the goal. For instance, the following jointed structure which is rotated back on itself.

We want to get to here:

If we try an alternative starting point, but this will go to the first situation.

The following starting point will converge provided that the link attached to the base is moved first.

I am trying to understand why this sometimes converges to the wrong point. Imagine that the following graph represents the angle of the first arm (across the screen) and the angle of the second arm (into the screen) and the height represents the distance from the required end point, which is a function of the two angles. Imagine that we are currently at the yellow spot. If we just change angle 1 (blue line) then the distance will always increase as we move from the yellow spot. Similarly if we just change angle 2 (green line) then the distance will always increase as we move from the yellow spot. So just changing one angle wont decrease the distance, but if we could change both angles simultaneously then we could lower the distance.

So how can we get out of this local minima? It seems to me that we first need a method to detect that we are not converging. If this is detected then we could try coupling the movements (either a positive change to angle 1 happens at the same time as a positive change to angle 2 or a positive change to angle 1 happens at the same time as a negative change to angle 2). An alternative approach would be that if we detect a local minima, then we randomise all the angles to see if we can converge from a different direction.