Maths - Lagrange Multipliers

This is a method to find maxima and minima of differential equations, of 2 or more variables, which are subject to constraints.

If we have 2 equations of these variables:

to find stationary points of f(x,y)

given

g(x,y) =0

One method is to subsitute for one of the variables, then differentiate to find the stationary points. But the functions may be too complex to easily do this substitution. Lagrange Multipliers provide a way to find the stationary points of simultanous equations without subsituting.

To find the stationary points of f(x,y) subject to the constraint g(x,y) = 0

For f(x,y) to be stationary -

this means:

The differential of g(x,y) is:

adding f to g times a constant gives:

We then choose the constant such that:

These last 2 equations and g(x,y) should allow the stationary points to be determined.

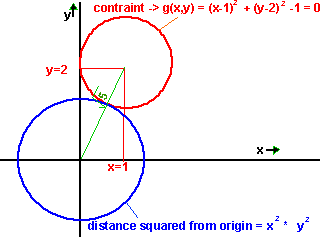
Example: Find the position of the nearest and furthest point from the origin, of a unit circle centered at x=1 and y=2. This can be found easily enough using geometry, since these points are on an extension of a line from [0,0] to [1,2]. the points reqired are at: as derived from the following diagram: So now we can solve the problem using Lagrange Multipliers to prove that it works: We are trying to find the maxima and minima of: The constaint is: So the partial differentials of these functions are: So using Lagrange Multipliers gives: 2x + (2x-2) =0 2y+ (2y-4) =0 Substituting gives: x=y/2 Expanding the constraint gives: x-2x+1+y-4y+4-1=0 substituting x=y/2 gives: y/4 -y + y-4y+4=0 y(5/4) - 5y + 4=0 Applying the quadratic formula gives: y = 2 +- 2/5 * sqrt(5) which gives the stationary points as expected:

EuclideanSpace

home

Problem Solving