In order to understand calculus on vectors we need to understand Scalar and Vector Fields.
Fist, on this page, we will look at differentiation with respect to some factor that is independant of space such as time (in classical mechanics) then we go on to look at calculus with respect to the dimensions of the space itself such as grad, div and curl.
Vector Differentiation with respect to a scalar
Since division of one vector by another is not generally valid we can't define differentiation with respect to another vector. Differentiation with respect to a scalar is defined as follows, if:
f(x) = [a , b , c , e]
then:
d f(x) / dx = [d(a /dx) , d(b/dx) , d(c/dx) , d(e/dx)]
In other words to differentiate with respect to a scalar, we just differentiate the elements individually. So to give a more specific example if:
f(x) = [xn , sin(x) , tan(x) , ex ]
then:
d f(x) / dx = [n*xn-1 , cos(x) , sec2(x) , ex ]
So this is quite simple, provided that we can differentiate the elements of a vector, we can differentiate the whole quaternion.
Although there is not a general vector division there are specific cases which allow us to differentiate one vector with respect to another and these correspond to specific types of vector differentiation known as grad, div and curl. We will discuss these after we have reviewed scalar and vector fields.
Scalar Field
We could represent how some scalar quantity, for example temperature, is defined for each point in the space.
We could define a function to show this, temp = f(x,y,z)

One way to illustrate this is to join up all the points with the same values. This is known as contour lines, or isothermals, or isobars, or whatever the name is that is appropriate to the scalar quantity.
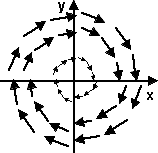
Vector Field
A vector field gives the value of a vector,for example velocity, for every position in the 2D or 3D space.
For example the following vector field might represent a velocity field for a rotating object.
Grad, Div and Curl
For information about grad, div and curl see the linked pages.
Identities


