Maths - Hemisphere Model

In the projective domain the length of the vector is less important because the projection onto the euclidean domain depends on the direction of the vector and not its length. There are different ways to deal with this redundant information about the length of the vector in the projective plane. We can call these models:

• hemisphere - normalise it to unit sphere centred at origin.
• stereographic - normalise it to unit sphere centred at z=1.

There are pros and cons of these two methods:

The first model seems more natural because rotations of the vector will automatically retain its unit length, but we are only using half the sphere and so we assume that opposite points on the sphere represent the same point in euclidean space.

here we look at the properties of the hemisphere model.

In order to illustrate the properties of this model we will use a two dimensional plane mapped onto three dimensional projective space.

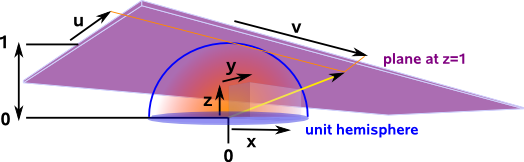
Here (u,v) represents the coordinates on the plane and (x,y,z) represents the cordinates in projective space (normalised to a unit sphere).

So to convert from euclidean coordinates to projective (hemisphere model) coordinates we have:

x y z

= 1/√(1 + u² + v²)

u v 1

and to convert from projective (hemisphere model) coordinates to euclidean coordinates we have:

u v

=

x/z y/z

Both these mappings are derived for this two dimensional case on this page.

We can see from the plot below that angles are not preserved by this mapping. We have a rectangular grid of red and blue lines on the plane, when we map these onto the hemisphere we see that:

• at he centre of the hemisphere the projected lines are rectangular.
• as we move outwards the red & blue lines no longer meet each other at 90°.

Infinity

Let us take the 2D (3D in projective space) case.

First horizontal lines, in this case u=∞ which gives,

x y z

= 1/√(1+u²+v²)

u v 1

=

u/√(1+u²+v²) v/√(1+u²+v²) 1/√(1+u²+v²)

=

1/√(1/u²+1+v²/u²) v/u√(1/u²+1+v²/u²) 1/u√(1/u²+1+v²/u²)

so substituting u=∞ gives,

=

1/√(0+1+0) v/∞√(0+1+0) 1/∞√(0+1+0)

=

1 0 0

so for horizontal lines they meet at:

1 0 0

For vertical lines, in this case v=∞ which gives,

x y z

= 1/√(1+u²+v²)

u v 1

=

u/√(1+u²+v²) v/√(1+u²+v²) 1/√(1+u²+v²)

=

u/v√(1/v²+1+u²/v²) 1/√(1/v²+1+u²/v²) 1/v√(1/v²+1+u²/v²)

so substituting v=∞ gives,

=

1/∞√(0+1+0) v/√(0+1+0) 1/∞√(0+1+0)

=

0 1 0

so for vertical lines they meet at:

0 1 0

EuclideanSpace

home

Transforms

Lie Group