There are various starting points to this subject of Minkowski Space:
- Defining a space formed from dimensions which either square to a positive or negative value.
- Defining the distance or metric of the space, in this case Minkowski metric or 'interval'
- Defining in physical terms as space-time.
Since these approaches all lead to the same results I suggest looking at them all on this page to see what you are most comfortable with.
| distance squares to +ve | time squares to +ve | |
|---|---|---|
| signature | +++- | ---+ |
| interval | √(Δx²+Δy²+Δz²-Δt²) | √(-Δx²-Δy²-Δz²+Δt²) |
| space like | Δx²+Δy²+Δz²>Δt² | Δx²+Δy²+Δz²<Δt² |
| time like | Δx²+Δy²+Δz²<Δt² | Δx²+Δy²+Δz²>Δt² |
| light like | Δx²+Δy²+Δz²=Δt² | Δx²+Δy²+Δz²=Δt² |
note: assumes dimensions which make c=1
Relationship To Space-Time
Minkowski Space is the geometry of space-time, that is a geometry which has 3 dimensions of space and one dimension of time. Usually we consider space dimensions to square to a positive real value and time to square to a negative real value (signature +++-) but some physicists find it useful to consider space dimensions to square to a negative real value and time to square to a positive real value (signature ---+) in some contexts.
In Euclidean space (where both axes square to the same value) then we can rotate the basis vectors and the algebraic structure, as shown by the Cayley tables, will remain the same. So there is a symmetry and the basis are arbitrary provided that we are consistent about it.
In Minkowski space (where axis square to different values) there is only one rotation that gives an orthonormal basis (standard diagonalised form).
Distance or Interval
We have discussed the Minkowski metric on this page.
We can define the geometry of this space by defining 'distance' this is the metric of a space, in this case the Minkowski metric, since our dimensions include both space and time we use the term 'interval' to specify the distance in space and time.
Although we are dealing with a 4 dimensional space-time this is difficult to understand so lets start with a simpler 2 dimensional case where the x dimension squares to +ve, the y dimension squares to -ve, and we will add a third dimension to show the distance from the origin. The resulting 'interval' is a complex number but either the real or the imaginary will be zero at any given point:
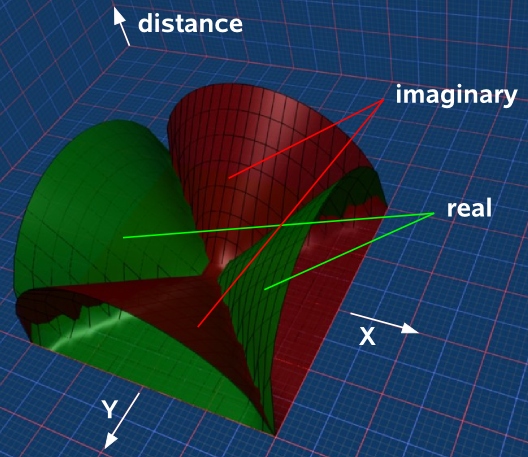
In Euclidean space:
- When we plot points on a grid this gives us information about the distance between the points.
In Minkowski space
- When we plot events on a grid the distance between the events on the grid is not necessarily a measure of the 'interval' between the points.
The way that we define distance is important because, for instance, a straight line is defined as the shortest distance between two points. If we know what is a straight line then we know the 'curvature' of the space. Minkowski space is hyperbolic.
In the above two dimensional case the distance measure is:
Δs = √(Δx²-Δy²)
In 4D space-time the interval is:
interval = √(Δx²+Δy²+Δz²-Δt²)
So how do we use this measure to define the concept of a straight line and to define how Minkowski space is curved?

On the metric page we came across a problem attempting to use this distance measure to define a straight line. In the above diagram the shortest distance between 'A' and 'B' would seem to be zero if we go via the origin? But if we allow this then the shortest distance between any two points is zero because we can always zigzag along diagonals.
To do this would involve going backwards and forwards in time, so perhaps our 'lines' need to be one directional to avoid this zigzaging? If we want to say: predict the path of particles/photons either forward or backward in time.
Squaring Vectors
In the algebras that we are investigating, the Cayley table shows that squaring individual vector basis gives a scalar value, because all terms on the leading diagonal are scalar values. For example:
e1²=+1
or e3²=-1
Will any value in this algebra square to a scalar value? For instance if
e1²=+1 and e2²=+1 then what happens if we square a linear combination of:
(a e1 + b e2)²
where:
- a and b are scalar multipliers.
- e1 and e2 are vector bases that individually square to +1
Squaring out the terms gives:
a²e1²+ a*b e1e2+ a*b e2e1 + b²e2
If the terms anticommute, that is: e1e2= -e2e1 then the middle terms will cancel out so we will get:
a²e1²+ b²e2
which will give a scalar value because the terms individually square to scalar values.
So, if terms anticommute then a linier sum of them will always square to a scalar value.
Distance Between Points
We want to investigate the effect of changing the basis but we need certain properties to remain the same, such a the distance between points on a solid object,
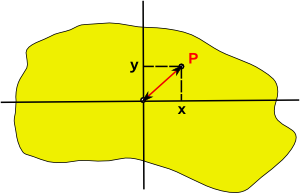
If the point P is given by:
xe1+ ye2
Then the square of the distance between P and the origin is given by:
x²e1²+ y²e2²
If we now choose different basis vectors the point P will now be given by:
x'e3+ y'e4
Then the square of the distance between P and the origin is given by:
x'²e3²+ y'²e4²

so for the distance to be the same in both cases:
x²e1²+ y²e2² = x'²e3²+ y'²e4²
Null Vectors, Idempotents and Nilpotents
Imagine that we have one dimension that squares to positive e1 (a space dimension) and another dimension that squares to negative e2 (a time dimension)

In between the dimension that squares to positive and the dimension that squares to negative there must be dimensions that squares to zero:
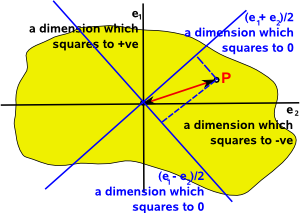
So how do we rotate the basis vectors in this case? In Euclidean space (where both axes square to the same value) then we can rotate the basis vectors as follows:
|
= |
|
|
So what is the equivalent in Minkowski space (where axis square to different values)? is there a hyperbolic equivalent?:
|
= |
|
|
Anyway, it we set θ=45° we get:
- n+ = (e1 + e2)/√2
- n- = (e1 - e2)/√2
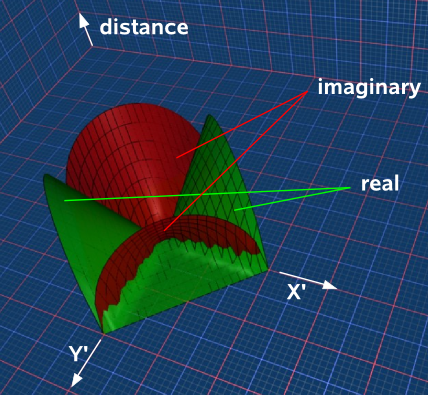
or inverting to get ex in terms of nx we can add both sides of the above equations:
n+ + n- = (e1 + e2+ e1 - e2)/√2 = √2 e1
and subtracting the above equations gives:
n+ - n- = (e1 + e2- e1 + e2)/√2 = √2 e2
So ex in terms of nx is:
- e1= (n+ + n-)/√2
- e2= (n+ - n-)/√2
So if a section of the Cayley table for e1 and e2 is:
a*b |
b.e1 | b.e2 |
| a.e1 | 1 | e1e2 |
| a.e2 | -e1e2 | -1 |
(it is only a section of the Cayley table because I have not included row and column for scalar term although it is in table)
So e1 squares to +ve and e2 squares to -ve and e1 anticommutes with e2. When we change the basis to n+ and n- the products are:
n+n+=(e1 + e2)(e1 + e2)/2 = (e1e1 + e1e2 - e2e1 + e2e2)/2 = 0
n+n-=(e1 + e2)(e1 - e2)/2 = (e1e1 - e1e2 - e1e2- e2e2)/2
= (1 - e1e2 - e1e2+ 1 )/2 = (2 - 2e1e2)/2 = 1 - e1e2
= 1 - (n+ + n-)(n+ - n-)/2 = 1 - (n+n+ - n+n- + n-n+ - n-n-)/2
= 1 + (n+n- - n-n+)/2
n-n+=(e1 - e2)(e1 + e2)/2 = (e1e1 + e1e2 + e1e2- e2e2)/2
= (1 + e1e2 + e1e2+ 1 )/2 = (2 + 2e1e2)/2 = 1 + e1e2
= 1 + (n+ + n-)(n+ - n-)/2 = 1 + (n+n+ - n+n- + n-n+ - n-n-)/2
= 1 + ( n-n+ - n+n-)/2
n-n- = (e1 - e2)(e1 - e2)/2 = (e1e1 - e1e2 + e1e2+ e2e2)/2 = 0
putting these into a Cayley table gives:
a*b |
b.n+ | b.n- |
| a.n+ | 0 | 1 + (n+n- - n-n+)/2 |
| a.n- | 1 + (n-n+ - n+n-)/2 | 0 |
Note that this Cayley table has a completely different structure to the tables that we have worked with upto now in that:
- The the type cant be found when combining tables by using the Kronecker Product.
- The basis n+and n- neither commute nor anti-commute so n+n- and n-n+ are different bi-vectors.
So I'm not yet sure how to work with this?
To Do s
There are a lot of question marks and potential errors on this page.
When this is done it would be nice to link to Special Relativity topics:
- Lorentz Transform
- Wick Rotation
- Boost
- Wave Functions
It would also be good to attempt to relate to other Cayley tables with zero entries such as those derived from dual numbers.

