On this page we discuss how to extend the scalar functions (that we discussed on this page) to the situation where the domain and/or codomain are complex numbers, we also discuss functions like normalise which are specific to complex numbers.
- Conjugate
- Powers of complex numbers
- Exponential Function
- log Function
- Inverse Function
- Reflection in circle
- Norm (normalise)
We can categorise these functions according to the the following properties:
- Conformal - preserves angles
- Anticonformal - reverses angles
- Non-conformal - does not conserve angles
| preservation of angles | preservation of distances | Analytic | |
|---|---|---|---|
| Conjugate | Anticonformal | ||
| Powers of complex numbers | |||
| Exponential Function | Riemann surface | ||
| Inverse Function | Conformal | yes, except at 0 and &in | |
| Reflection in circle | Anticonformal | ||
| Norm (normalise) | |||
| Möbius transformation |
Evaluating Complex Functions
We can evaluate the value of many complex functions by using infinite series in the same way that we can for scalar functions. We just use the same series that we would use for scalar functions but plug in complex values instead of real values. So if a series exists for real values we can evaluate the complex function. For example:
| ln(1+z) | z - z 2/2! + z 3/3! ... +(-1)r+1zr/(r)! | -1 < z <= 1 |
| exp(z) | 1 + z 1/1! + z 2/2! + z 3/3! ... + zr/(r)! | all values of z |
Alternatively we can derive the real and imaginary parts in terms of the real functions:
| function of complex variable | real and imaginary terms |
|---|---|
| exp(x+i y) | exp(x)*(cos(y)+i sin(y)) |
| ln(x+i y) | 0.5*ln(x²+y²) + i atan(x/y) |
| sin(x+i y) | cosh(-y) sin(x) - i sinh(-y) cos(x) |
| cos(x+i y) | cosh(-y) cos(x) + i sinh(-y) sin(x) |
| tan(x+i y) | (tan(x) -i tanh(-y)) / |
| sinh(x+i y) | sinh(x) cos(y) + i cosh(x) sin(y) |
| cosh(x+i y) | cosh(x) cos(y) + i sinh(x) sin(y) |
| tanh(x+i y) | (tanh(x) + i tan(y)) / (1 +i tanh(x) tan(y)) |
We can convert between the circular and hyperbolic functions as follows:
- sin(z) = -i sinh(iz)
- cos(z) = -cosh(iz)
- tan(z) = -i tanh(iz)
See also the trig identities on this page.
Conjugate
When we multiply a complex number by its conjugate we get a real number, in other words the imaginary part cancels out.
Inverse Function
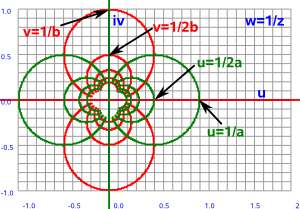
To calculate the inverse value (1/z) we multiply the top and bottom by the conjugate which makes the denominator a real number.
| z plane | w plane | |
|---|---|---|
 |
--> w=1/z |
|
Let the components of the input and output planes be:
z = x + i y and w = u + i v
In this case w = 1/z
so:
w = 1/(x + i y)
As usual, we evaluate the inverse by multiplying top and bottom by the conjugate:
w = (x - i y)/(x + i y)(x - i y)
w = (x - i y)/(x² + y²)
so the u and v components are:
u = x /(x²+y²)
v = -y /(x²+y²)
This function has some very interesting and useful properties:
- Straight lines through the origin map to themselves.
- Straight lines not through the origin map to circles.
- Circles through the origin map to straight lines.
- Circles not through the origin map to circles.
- Applying the inverse function twice restores the original.
- The inverse function can be decomposed into a conjugate and a reflection in a circle.
So this function can be used to map between circles and lines. We can also extend the concept to 3 dimensions which allows us to map the surface of a sphere to the plane (see stereographic projections).
Möbius Transform
This can be generalised to the Möbius Transform (described here):
![]()
Where:
- z = input (complex values)
- w = output (complex values)
- a,b,c,d = parameters (complex values)
The inverse function is a special case where a=d=0 and b=c=1 we get:
w=1/z
If we now allow d to be non-zero we can see that this will just shift the line in the z-plane:
w=1/(z+d)
If we now allow c to scale we can see that this will scale the position on the line in the z-plane:
w=1/(cz+d)
If we now allow a and b to vary things get a bit more complicated but we can see that we can move the circle around the w plane.
Exponential Function
There are two methods to calculate the exponential function:
- polar form and Euler's equation as discussed on this page.
- infinite series as discussed on this page.
| z plane | w plane | |
|---|---|---|
 |
--> w=ez |
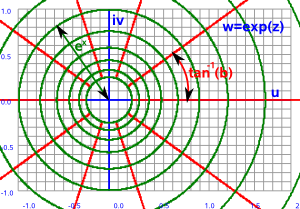 |
Let the components of the input and output planes be:
z = x + i y and w = u + i v
In this case w = ez
so:
w = e(x + i y)
by the rules of exponents:
w = exei y
applying Euler's equation we get:
w = ex(cos(y) + i sin(y))
so the u and v components are:
u = excos(y)
v = exsin(y)
Log Function
The natural log, that is the log to the base e, is the inverse of the exponetial function. So if,
w = ln(z)
then taking the exponent of each side gives,
ew = z
so we have
x = eucos(v)
y = eusin(v)
which gives:
u = ln(√(x² + y²))
v = atan(x/y)
Powers of complex numbers
Here is the plot for (x + i y)² the more general expression for (x + i y)n is given on this page.
| z plane | w plane | |
|---|---|---|
 |
--> w=z² |
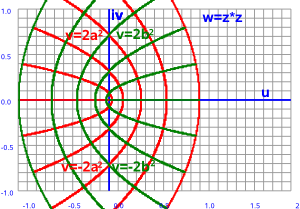 |
Pure real values always square to a positive value and pure imaginary values always square to a negative value. However real and imaginary parts together cover the whole plane.
Let the components of the input and output planes be:
z = x + i y and w = u + i v
lets take the example of the square function w = z²
so:
w = (x + i y)²
multiplying out gives:
w = x² - y² + i 2 x y
so the u and v components are:
u = x² - y²
v = 2 x y
Norm
This is the distance (r) of a + i b from the origin.
It is written as:
r = | a + i b |
by Pythagoras:
r = | a + i b | = math.sqrt(a*a + b*b)
Check that:
|a + i b|*|c + i d| = |a*c - b*d + i (a*d + b*c)|
Möbius transformation
The mapping between the surface of the sphere and the plane can be represented by the Möbius transformation of the form:
| M(z)= | az + b |
| cz + d |
Where:
- z = complex variable
- a,b,c & d = complex constants
This is useful in the stereographic projection explained on this page.
Further Study
I think its interesting to compare these graphs for complex numbers to the equivalent graphs for double numbers and dual numbers.