Maths - Generating Hypercomplex Numbers

We can create various trees of algebras starting with 2 dimensional complex-number like (complex, double and dual) algebras and doubling up more and more algebras of 2,4,8,16… dimensions. So we start with one of these:

designation multiplication table type
C
1 i
i -1
complex
Do
1 D
D 1
double
Du
1 e
e 0
dual

Like the Clifford algebras these are characterised by what they square to, 'C' squares to -1, 'Do' squares to +1 and 'Du' squares to 0. Starting with these 2D algebras we can double up to form a whole hierchy of algebras:

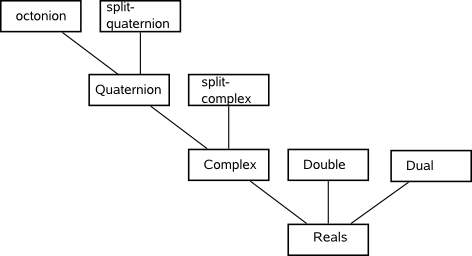
tree of cayley-dickson trees

When we combine two 2D algebras to form a 4D algebra (say combine a complex number with another complex number to form a quaternion) what we are really doing is taking the complex number but instead of its elements being real numbers we make its elements themselves complex numbers, or alternativly, if we start with a complex number and allow each of its elements to be a double number the we get 4D split-complex numbers. We can then go on to the 'n'th level so on to form an algebra with dimension 2n and so on.

This gives us a sort of 'algebra factory' to produce the algebra with the dimension and the properties that we want. However there are at least 3 (possibly more) different trees that we can produce depending on the exact rules that we use.

  1. The Cayley-Dickson construction
    this builds, complex-numbers,quaternions, octonions, sedenions...
    by using multiplication, for instance,
    H = C*C
    O=H*H
    and so on. ( Musean hypernumber, M-algebra?)
  2. Clifford Algebra
    As (2) but instead of treating i^j as creating a new vector dimension we treat it as creating a bivector dimension and so on with higher 'blades'.
  3. Matrix Algebra
    Where det(M) = +1 and [M][M]t=1
    Although we increase the dimension by adding a row and column we can also use Kronecker product.

The algebras are like leafs on these trees, but a particular algebra may not be unique to a given tree, so the trees join up. For instance C and H are even sub-algebras of particular Clifford Algebras. Where the trees join does not seem to have a totally predicable pattern but there is a periodicity of 8.

We can also combine algebras across these groupings, for example, SU(n) is often defined as an n dimensional matrix where each element of the matrix is a complex number.

Cayley-Dickson Doubling Process.

This builds, complex-numbers,quaternions, octonions, sedenions...

 

The multipication table for complex numbers is:

(a+ i b)*(c+ i d) c d
a ac ad
b cb -db

However, if a,b,c and d are not real numbers but are higher order elements, such as complex numbers, we need to modify the table slightly (the modification has no effect on real numbers):

(a,b)(c,d) c d
a ac a*d
b cb -db*

where:

Alternativley the Cayley-Dickson construction is often expressed in these terms:

(a,b)(c,d) = (ac - db* , a*d + cb)

For more about Cayley-Dickson construction see this page.

Cayley-Dickson related to Cayley Table

On this page we discussed algebras where the rules to multiply terms such as:

we could detemine the product of these terms by:

(a ei)*(b ej) = a*b*Sij*(ei⊗ej)

where:

So to build the Cayley table we need to calculate the type and sign of each term.

The type is relaively easy provided that the terms are ordered in bit order, that is, 0=real value and the other values are vector bases in the order that the terms are combined. In this case the type is represented by the Kronecker product which can be calculated from the bitwise exclusive or.

The sign can be calculated directly from the Cayley table, for example we will double up a quaternion to give an octonion, using the Cayley-Dickson formula in Cayley Table form:

  C D
A AC DA
B BC' -D'B

The signs for the unmodified terms are given by the sign values for quaternion:

AB=AD=BC=BD
+ + + +
+ - + -
+ - - +
+ + - -

To reverse the order of the operands we swap the terms across the leading diagonal, ie swap the red and yellow boxes here:

BA=
+ + + +
+ - - +
+ + - -
+ - + -

Or to take the cojugate of one of the terms invert all but the first row or column:

BC'=
+ - - -
+ + - +
+ + + -
+ - + +

So the quadrants in the table we need are:

AB=
+ + + +
+ - + -
+ - - +
+ + - -
       
AD=
+ + + +
+ - + -
+ - - +
+ + - -
DA=
+ + + +
+ - - +
+ + - -
+ - + -
   
BC
+ + + +
+ - + -
+ - - +
+ + - -
BC'=
+ - - -
+ + - +
+ + + -
+ - + +
   
-BD
- - - -
- + - +
- + + -
- - + +
-DB
- - - -
- + + -
- - + +
- + - +
-D'B
- + + +
- - - +
- + - -
- - + -

Putting them all together gives the full sign table for the octonion:

O=H⊗H
C
D
A + + + + + + + +
+ - + - + - - +
+ - - + + + - -
+ + - - + - + -
B + - - - - + + +
+ + - + - - - +
+ + + - - + - -
+ - + + - - + -

Cayley-Dickson Cayley Table
(a0,a1)(b0,b1) =
(a0 b0 - b1 a1' , a0' b1 + b0 a1)
  b0 e0 b1 e1
a0 e0 a0 b0 e0 a0' b1 e1
a1 e1 b0 a1 e1 -b1 a1' e0
Cayley-Dickson Cayley Table

(A0,A1)(B0,B1) =
(A0 B0 - B1 A1' , A0' B1 + B0 A1)

where:

A0 = (a00,a01)
A1 = (a10,a11)
B0 = (b00,b01)
B1 = (b10,b11)

(A0,A1)(B0,B1) =
((a00,a01),(a10,a11))((b00,b01),(b10,b11)) =

((a00,a01) (b00,b01) - (b10,b11) (a10,a11)' ,
(a00,a01)' (b10,b11) + (b00,b01) (a10,a11))

multiplying out the terms and let (x,y)' = (x,y') gives:

=(a00 b00 - b01 a01' , a00' b01 + b00 a01)
- (a10 b10 - b11 a11' , a10' b11 + b10 a11'),
(a00 b10 - b11 a01' , a00' b11 + b10 a01')
+ (a10 b00 - b01 a11' , a10' b01 + b00 a11)

which gives the four terms:

=(a00 b00 - b01 a01' - a10 b10 - b11 a11',
a00' b01 + b00 a01 + a10' b11 + b10 a11',
a00 b10 - b11 a01' + a10 b00 - b01 a11',
a00' b11 + b10 a01' +a10' b01 + b00 a11)

 

  b0 e0 b1 e1 b0 e0 b1 e1
a0 e0 a0 b0 e0 a0' b1 e1 a0 b0 e0 a0' b1 e1
a1 e1 b0 a1 e1 -b1 a1' e0 b0 a1 e1 -b1 a1' e0
a0 e0 a0 b0 e0 a0' b1 e1 a0 b0 e0 a0' b1 e1
a1 e1 b0 a1 e1 -b1 a1' e0 b0 a1 e1 -b1 a1' e0

 

 

Construct from Kronecker product

 

For example we could generate C⊗C as follows: first we take C given by:

1 i
i -1

We want to combine this with another copy of 'C', this requires another independent dimension so this time we will use j instead if i:

1 j
j -1

We combine these using the Kronecker product, by taking all combinations of i and j, that is: 1, i, j, i^j. Then put in 4×4 array going across the table (red) and down (blue) which gives:

1^1 1^i 1^j 1^i^j
i^1 i^i i^j i^i^j
j^1 j^i j^j j^i^j
i^j^1 i^j^i i^j^j i^j^i^j

We can simplify this by using the individual tables to give us the following identities:

Which gives:

1 i j i^j
i -1 i^j -j
j -i^j -1 i
i^j j -i -1

This is exactly the same as G 0,2,0 which is a geometric algebra based on two dimensions which both square to -ve, shown here:

e e1 e2 e12
e1 -e e12 -e2
e2 -e12 -e e1
e12 e2 -e1 -e

This table was generated using the program described on this page

Its not surprising the table is the same (with only notation differences) as is was derived in the same way.

But here is where the division algebras diverge from geometric algebra, in geometric algebra terms like i^i are called bivectors and remain in that form as they can't be simplified any further, in division algebras like this we convert the bivector terms into vectors like this:

let k=i^i

This gives,

1 i j k
i -1 k -j
j -k -1 i
k j -i -1

If we only did this at the end of the calculation it would not matter since we have already shown that:

C⊗C = H = G 0,2,0

But we are going on to build up further algebras from this and since the vector base k has slightly different properties to the bivector base i^i then the algebras are going to diverge more and more as we build up more complex algebras.

For instance, if we add another multiplication by C to give octonions,

C⊗C⊗C = O

This can cause non-associativity because the⊗operator involves converting bivector bases to vector bases and vector×bivector may involve a sign change from bivector×vector. So it may be that:

(C⊗C)⊗C ≠ C⊗(C⊗C) ?

This may become even more ambiguous for 16ions, do we define them as (C⊗C)⊗(C⊗C) or C⊗(C⊗C)⊗C ?

We can calculate the result as follows:

The terms of C⊗C are 1,i,j,k and we will multiply this by a third complex number, say,

1 m
m -1

which gives the product:

1^1 1^i 1^j 1^k 1^m 1^i^m 1^j^m 1^k^m
i^1 i^i i^j i^k i^m i^i^m i^j^m i^k^m
j^1 j^i j^j j^k j^m j^i^m j^j^m j^k^m
k^1 k^i k^j k^k k^m k^i^m k^j^m k^k^m
m^1 m^i m^j m^k m^m m^i^m m^j^m m^k^m
i^m^1 i^m^i i^m^j i^m^k i^m^m i^m^i^m i^m^j^m i^m^k^m
j^m^1 j^m^i j^m^j j^m^k j^m^m j^m^i^m j^m^j^m j^m^k^m
k^m^1 k^m^i k^m^j k^m^k k^m^m k^m^i^m k^m^j^m k^m^k^m

simplifying gives:

1 i j k m i^m j^m k^m
i -1 k -j i^m -m k^m -j^m
j -k -1 i j^m -k^m -m i^m
k j -i -1 k^m j^m -i^m -m
m -i^m -j^m -k^m -1 i j k
i^m m -k^m j^m -i -1 k -j
j^m k^m m -i^m -j -k -1 i
k^m -j^m i^m m -k j -i -1

again we convert bivectors to vectors as follows:

i =e1, j=e2, k=e3, m=e4, i^m=e5, j^m=e6, k^m=e7

which gives:

1 e1 e2 e3 e4 e5 e6 e7
e1 -1 -e3 e2 -e5 e4 e7 -e6
e2 e3 -1 -e1 -e6 -e7 e4 e5
e3 -e2 e1 -1 -e7 e6 -e5 e4
e4 e5 e6 e7 -1 -e1 -e2 -e3
e5 -e4 e7 -e6 e1 -1 e3 -e2
e6 -e7 -e4 e5 e2 -e3 -1 e1
e7 e6 -e5 -e4 e3 e2 -e1 -1

which is the multiplication table for octonions.

I have not yet worked out the table when the terms are combined in a different order, my plan is to adapt the program here to do this. Such a program would become more necessary as we build really big algebras (for example E8).

For more about Kronecker product construction see this page.

Clifford Algebras

Here we investigate how Clifford and these Division Algebras are related. I think this is an important question because these division algebras tend to be treated by mathematicians as a subset of the study of Clifford Algebra.

On this page we saw how we can generate a geometric algebra from its signature of the form: Gp,q,r

where:

We can take subsets of these algebras, denoted as follows:

metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

 

cover us uk de jp fr ca On Quaternions and Octonions

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.