This page overlaps with the page here, I need to combine them.
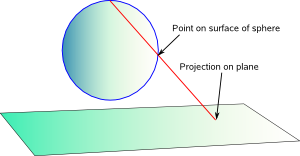
Projecting surface of sphere onto plane
We can represent any point on a sphere by using a complex number.
When we were looking at complex functions we saw that for inversions:
(w = 1/z) then:
- Straight lines through the origin map to themselves.
- Straight lines not through the origin map to circles.
- Circles through the origin map to straight lines.
- Circles not through the origin map to circles.
- Applying the inverse function twice restores the original.
- The inverse function can be decomposed into a conjugate and a reflection in a circle.
So this function can be used to map between circles and lines. We can also extend the concept to 3 dimensions which allows us to map the surface of a sphere to the plane.
The mapping between the surface of the sphere and the plane can be represented by the Möbius transformation of the form (Möbius transformations are described on this page)
| M(z)= | az + b |
| cz + d |
Where:
- z = complex variable
- a,b,c & d = complex constants
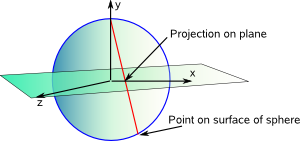
To simplify things we will now place the plane through the centre of the sphere and we change the notation slightly:
- π = points on surface of sphere represented as a plane (complex number).
- x,y,z = three dimensional coordinates.
This gives the representation of a point on the sphere as:
| π(x,y,z)= | x + i z |
| 1-y |
Examples:
point at south pole = (0,-1,0)
| π(x,y,z)= | 0 | = | 0+ 0 i |
| 2 |
point at north pole = (0,1,0)
| π(x,y,z)= | 0 | = | ∞ |
| 0 |
point at equator = (1,0,0)
| π(x,y,z)= | 1 | = | 1 + 0 i |
| 1 |
point at equator 90° = (0,0,1)
| π(x,y,z)= | i 1 | = | 0 + 1 i |
| 1 |
