The most intuitive way to begin to understand the a manifold is as an extension of the concept of surface to n dimensions (a hypersurface). More generally a manifold is a subset of 'n' dimensional Euclidean space, but not just any subset, an n-dimensional manifold is something which locally
looks like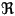 n. In other words, if you zoom in on a piece of your space,
it looks like
n. In other words, if you zoom in on a piece of your space,
it looks like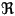 n.
n.
However we do not always want to define manifolds in terms of embedding them in some higher dimensional Euclidean space which leads to the following:
Definition :
An -dimensional topological manifold is a second countable Hausdorff space that is locally Euclidean of dimension n.
Examples:
An example of a 1-dimensional
manifold would be a circle, if you zoom around a point the circle looks like a line (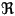 1).
1).
An example of a 2-dimensional
manifold would be a sphere, a small piece looks like a plane (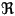 2).
2).
Topological Space
We want to study the properties of manifolds that are preserved by continuous maps, to do this we do not want to use the concept of distance (metric space) and yet we still need the concept of continuous functions to make sense.
To do this we use the concept of 'open space' and 'open set'. The notion of an open set provides a fundamental way to speak of distance in a topological space, without explicitly defining a metric on the space. In particular, although one cannot obtain concrete values for the distance between two points in a topological space, one may still be able to speak of "nearness" in the space, thus allowing concepts such as continuity to translate into the theory of open sets.
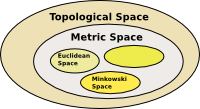
More about topological space on this page.
Hausdorff Space
A topological space is said to be a Hausdorff space if given any pair of distinct points p1, p2![]() H, there exists neighborhoods U1 of p1 and U2 of p2 with U1
H, there exists neighborhoods U1 of p1 and U2 of p2 with U1![]() U2 = Ø.
U2 = Ø.
In other words: open sets separate points.
Types of Manifold
A smooth manifold, which in addition to the above requires that the space be "smooth", i.e. have no corners, sharp edges, etc. The circle and sphere are such examples, a square is not.
Rotations and Manifolds
Rotations have a certain degree of freedom. In two dimensional space then rotation has one degree of freedom, in three dimensional space then rotation has three degrees of freedom. However, as we explained on this page, if we work purely in terms of the minimum number of dimensions then we are working with non-linear spaces with singularities and other problems, this leads to practical difficulties. One problem is that this makes it difficult to combine subsequent rotations into single equivalent rotation.
In order to linearise rotations we need to embed these dimensions (equal to the number of degrees of freedom) into a higher number of dimensions in order to straighten out and linearise the dimensions.
It would be good if we could use the mathematics of Manifolds to prove whether rotations can be represented linearly in a given number of dimensions. For instance in three dimensions, Euler angles are not linear and I don't beleive there is a way to modify them to make them linear, we have to go to four dimensional quaternions to do that. How do we prove that? I would appreciate any help.
2D Rotations
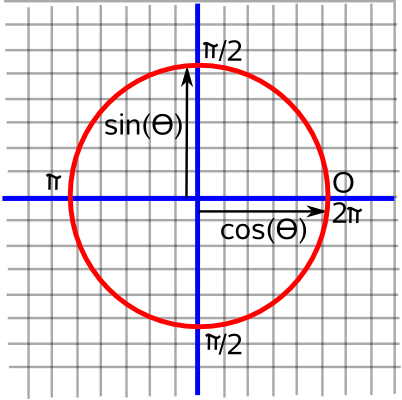
A rotation in 2 dimensions has one degree of freedom. That is we can represent any rotation by a single scalar value from 0 to 2π radians (360°)
![]()
This seems linear in that to combine rotations we just add them together (modulo 2π) but in other numbers of dimensions we combine subsiquent rotations by multiplying mathematical quantities (this is bilinear in that if we hold one of the quantities constant the other will follow a straight line graph). We can do this for 2D rotations by representing them by complex numbers this embeds a 1D quantity in a 2D space.
3D Rotations
We can represent 3D rotations by 3 angles, known as Euler angles, two of these angles goes from -π to π radians the other goes from -π/2 to π/2 radians.
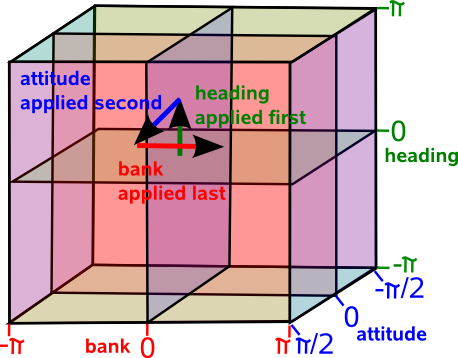
In the above diagram we show these 3 angles labeled here as "heading", "attitude" and "bank" but we have to be very carful with this diagram because we must always be consistant about the order that we apply the angles otherwise we will get different results.
In the example below we rotate heading 90° (2a) followed by attitude 90° (3a) and the aircraft is going up with the rudder pointing toward us, however if we rotate attitude 90° (2b) followed by heading 90° (3b) and the aircraft is going up with the rudder pointing away from us.
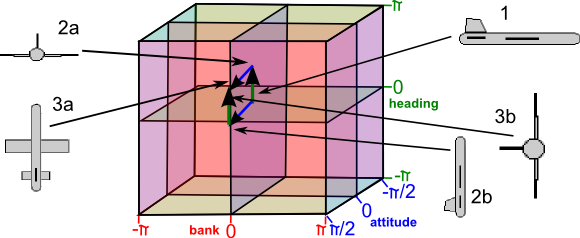
I think we can still use this diagram but we have to be careful to interpret it as implying an order and we cannot change the order. Also a given position in this space may not be the only place that that rotation is represented, for instance heading 90° then attitude 90° then heading -90°is equivalent to a single bank of 90°
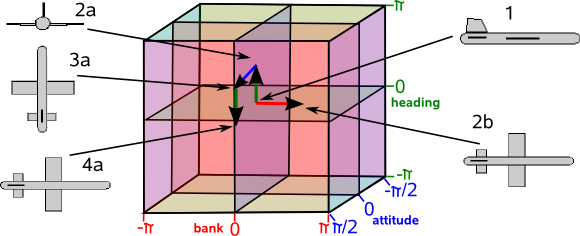
But again this is not valid on this diagram because we have altered the order of the Euler angles. All this really shows is that we cannot add the angles if we are combining them in different orders.
Even if we do apply the angles in our chosen order it does not necessarily mean that each point on the diagram represents a unique rotation, it may be that the same rotation is represented at several places on the diagram, this happens at the singularities attitude= ±π/2.
So can we distort this model so that it becomes linear?
Singularities
In mathematics there are different types of singularity, in these cases we are talking about the situation where:
- Many points in one representation are mapped onto a single point in another representation.
- Infinitesimal changes close to the singularity in one representation may cause large changes in the other representation.
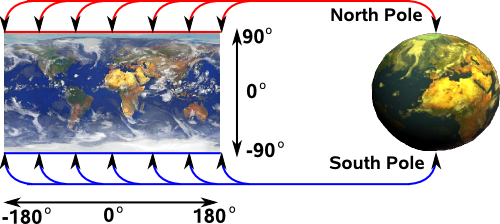
Projecting surface of sphere onto plane
The Mercator Projection maps the north and south poles to lines this means that, at these points, the projection is many to one (more about this subject on this page):
Singularities of Euler angles
Simarly we can map Euler angles to quaternions (4 dimensional hypersphere). This maps a one dimensional space (rotations around 0,1,0 axis) to a two dimensional plane in Euler terms. This is where attitude = 90° and heading, bank vary:
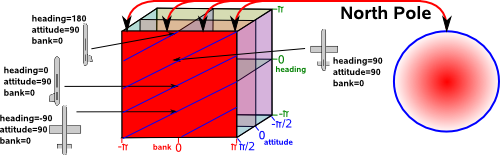
On this plane lines of common orientation are diagonal lines, that is rotation around 0,1,0 axis are given by angle = heading+bank.
Similarly for the south pole.

