Maths - Functions Of Dual Numbers

On this page we discuss how to extend the scalar functions (that we discussed on this page) to the situation where the domain and/or codomain are double numbers, we also discuss functions like normalise.

• Conjugate
• Powers of double numbers
• Exponential Function
• Inverse Function
• Norm (normalise)

Conjugate

As with complex numbers when we multiply a double number by its conjugate we get a real number, in other words the imaginary part cancels out. However the value is different:

for complex numbers: (a + i b)(a - i b) = a² + b²

for dual numbers: (a + ε b)(a - ε b) = a²

Inverse Function

To calculate the inverse value (1/z) we multiply the top and bottom by the conjugate which makes the denominator a real number.

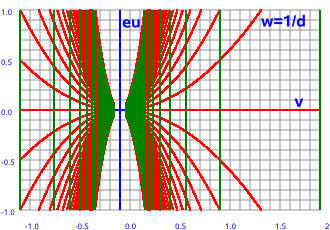
z plane		w plane
	--> w=1/z

how this plot was produced.

Let the components of the input and output planes be:

z = x + ε y and w = u + ε v

In this case w = 1/z

so:

w = 1/(x + ε y)

As usual, we evaluate the inverse by multiplying top and bottom by the conjugate:

w = (x - ε y)/(x + ε y)(x - ε y)

w = (x - ε y)/(x²)

so the u and v components are:

u = x /(x²)= 1/x
v = -y /(x²)

Evaluating Dual Functions

We can evaluate the value of many dual functions by using infinite series in the same way that we can for scalar functions, we just use the same series that we would use for scalar functions but plug in dual values instead of real values, so if a series exists for real values we can evaluate the dual number function. The higher order powers of ε will be zero so functions of ε are easy to calculate (see exponetial below).

Exponential Function

This is discussed when we discuss polar form and Euler's equation on this page.

z plane		w plane
	--> w=ez

how this plot was produced.

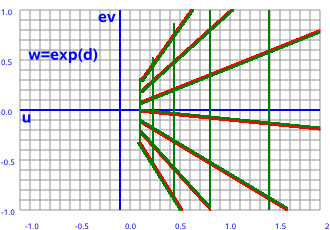Let the components of the input and output planes be:

z = x + ε y and w = u + ε v

In this case w = e^z

so:

w = e^{(x + ε y)}

by the rules of exponents:

w = e^xe^{ε y}

How do we evaluate this? I don't know of a version of Euler's equation which applies to dual numbers so we have to resort to infinite series:

e^x = 1 + x¹/1! + x²/2! + x³/3! ... + x^r/(r)!

e^{ε y}= 1 + (ε y) ¹/1! + (ε y)²/2! + (ε y)³/3! ... + (ε y)^r/(r)!

but terms containing ε² and higher terms are zero so we have:

e^{ε y}= 1 + ε y

w = e^x(1 + ε y)

which gives:

u = e^x
v = e^x y

Powers of dual numbers

z plane		w plane
	--> w=z²

how this plot was produced.

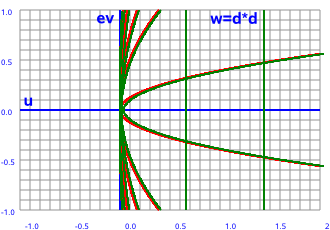Pure real values always square to a positive value and pure imaginary values always square to a negative value. However real and imaginary parts together cover the whole plane.

Let the components of the input and output planes be:

z = x + ε y and w = u + ε v

lets take the example of the square function w = z²

so:

w = (x + ε y)²

multiplying out gives:

w = x² + ε 2 x y

so the u and v components are:

u = x²
v = 2 x y

Norm

This is the distance (r) of a + ε b from the origin.

It is written as:

r = | a + ε b |

by Pythagoras:

r = | a + ε b | = math.sqrt(a*a + b*b)

Check that:

|a + ε b|*|c + ε d| = |a*c - b*d + ε (a*d + b*c)|

Further Study

I think its interesting to compare these graphs for complex numbers to the equivalent graphs for complex numbers and double numbers.

 

EuclideanSpace

home

Prerequisites

On this page we discussed how to represent and evaluate functions where the domain and codomain are complex numbers.

Transforms