 |
 |
 |
 |
 |
further reading | more topics » |
| mjbWorld program | 3D theory |
3D physics |
3D maths |
3D programming | technology |
about site |
sitemap A-Z |
| index | algebra | geometry | calculus | graph theory | statistics | principles | standards |
| index | equations | multi-dim | vector | matrix | complex | clifford | groups |
| common | concepts | 2D | 3D | 4D | 5D |
| index | basis | arithmetic | functions | affine | transform | code |
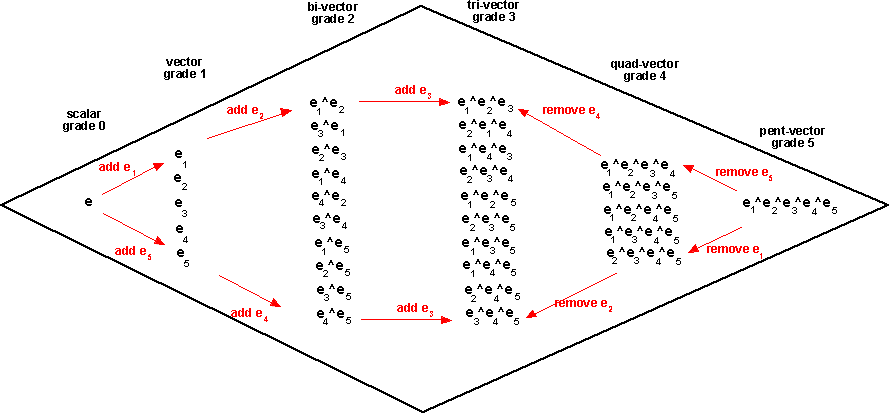
For 5 dimensions can be generated by 5 basis vectors, e1, e2, e3, e4 and e5
One of the most important applications of a Geometric Algebra based on 5D vector space is to represent conformal space.
In the case of conformal space e1, e2, e3, e0 and e∞ so e4 and e5 can be replaced by e0 and e∞ where:
:
| grade | base value | numerical value | |
|---|---|---|---|
full |
shortened |
||
| 0=unit scalar | 1 | e | |
| 1=unit length base vectors | e1 | e1 | |
| e2 | e2 | ||
| e3 | e3 | ||
| e4 | e4 | ||
| e5 | e5 | ||
| 2=unit length base bivectors | e1^ e2 | e12 | e12 |
| e3^ e1 | e31 | e31 | |
| e2^ e3 | e23 | e23 | |
| e1^ e4 | e14 | e14 | |
| e4^ e2 | e42 | e42 | |
| e3^ e4 | e34 | e34 | |
| e1^ e5 | e15 | e15 | |
| e2^ e5 | e25 | e25 | |
| e3^ e5 | e35 | e35 | |
| e4^ e5 | e45 | e45 | |
| 3=unit length base tri-vector | e1^ e2^ e3 | e123 | e123 |
| e2^ e1^ e4 | e214 | e214 | |
| e1^ e4^ e3 | e143 | e143 | |
| e2^ e3^ e4 | e234 | e234 | |
| e1^ e2^ e5 | e125 | e125 | |
| e1^ e3^ e5 | e135 | e135 | |
| e2^ e3^ e5 | e235 | e235 | |
| e1^ e4^ e5 | e145 | e145 | |
| e2^ e4^ e5 | e245 | e245 | |
| e3^ e4^ e5 | e345 | e345 | |
| 4=unit length base quad-vector | e1^ e2^ e3^ e4 | e1234 | e1234 |
| e1^ e2^ e3^ e5 | e1235 | e1235 | |
| e1^ e2^ e4^ e5 | e1245 | e1245 | |
| e1^ e3^ e4^ e5 | e1345 | e1345 | |
| e2^ e3^ e4^ e5 | e2345 | e2345 | |
| 5=unit length base pent-vector | e1^ e2^ e3^ e4^ e5 | e12345 | e12345 |
So in this case the number of dimensions is:
In this case the number of scalar values in the multivector is 32 = (1+5+10+10+5+1)
You may be interested in other means to represent orientation and rotational quantities such as:
Or you may be interested in how these quantities are used to simulate physical objects:
If you are not familiar with vectors this subject you may like to look at the following page first:
|
metadata block |
|
| see also: | |
| Correspondence about this page |
|
|
Book Shop - Further reading. Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them. |
|
|
Commercial Software Shop Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them. |
|
Can you help? Please send me any improvements to here. I would appreciate ideas to make the pages more useful including error correction, ideas for new pages, improvements to wording. It helps if you quote the full URL of the page. |
Could anyone let me know of a good proof that a quaternion multiplication can be used to represent a rotation in 3 dimensions, I'm not looking for the shortest proof, but the most easily understood. |
|
Terminology and Notation Specific to this page here: |
|
|
program I am working on a project which uses these principles, if you would like to help me with this you are welcome to join in, here: |
|
This site may have errors. Don't use for critical systems.
Copyright (c) 1998-2008 Martin John Baker - All rights reserved.
