This is part of some experimental code that I am writing to implement the FriCAS interpreter using SPAD code. For an overview of this experiment see page here. For information about how this is done using the current boot/lisp code see the page here.
The parser converts a list of tokens to a tree structure containing untyped values. The token list is created by the tokeniser as described on the page here.
| So a list of tokens like 2*(3+4) would be converted to a structure like: | 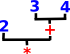 |
The existing boot code for this uses complicated recursive techniques. Of course these expressions are naturally recursively defined but the code goes to the extent of using a 'zipper' structure. I get the impression that this is intended to traverse the structure in a non mutable way without having any pointers. For a discussion of the existing boot code and the history of the Scratchpad/Axiom/FriCAS interpreter see the page here.
I am experimenting with writing such a parser in SPAD. So what are the aims:
- Maximum compatibility with the existing interpreter?
- Maximum compatibility with the existing compiler?
Well both of these things are important, I don't want to break existing stuff and it is annoying when the interpreter and compiler give different results.
However, for me, there is a requirement that is just as important as these: I want a firm basis for adding new capabilities (see my wishlist). A particularly relevant example here is 'per-domain operator precedence. I think this would be difficult to archive if the SPAD code was written using a line-by-line translation of the 'zipper' code.
Theory
The interpreter is used mostly for simple human and script input rather than defining domains and so on. So is a simple top-down parsing algorithm such as a recursive-descendent or LL(1) parser good enough? Also what type of algorithm is most efficient in an interpreter context?
- Can we drive the parser from a formal definition of the input? If so, can we use a context free grammar?
- Can we use an off-the-shelf parser generator? I suspect not because of my wish to have per-domain operator precedence.
As this is an experiment I will try to use a simple recursive-descendent parser but without using the 'zipper' approach in the existing parser.
Possible Algorithms
Some possible algorithms are discussed on the website here:
I did not want to use the 'shunting yard algorithm' because this builds in each operator as a hard coded function in the interpreter and this is a problem because I want to make the precedence more dynamic (see below). We therefore need the parser to be table driven.
So I would like to try something like what is described as 'Precedence climbing' on the above website.
Infix Operators
The most difficult part of this parsing is infix operators. As we step through the list of tokens we need to build up a tree. When we do this we need to take into account the precedence of the operators:
| In this case: when we get to '*' it has a higher precedence so we add an extra branch above (inside) the existing one. |  |
| In this case: when we get to '+' it has a lower precedence so we add an extra branch below the existing one. |  |
The problem (for my wish to have per-domain operator precedence) is that, at this stage, we have not established what types(domains) we are using so we don't know the precedences. I guess one possibility might be to do in once using the default precedence, then work out the types, then do it again with the correct precedence. I think this would get it right for most cases but there is a theoretical possibility that it might get it wrong.
Atomic Value Tree
This holds the output of the parser. The concept is similar to lisp SExpressions but I have used this instead to avoid reliance on building on top of lisp.
 |
Here leaves are atomic types which are one of:
Nodes are one of:
|
When parsing input it will only have 1 element of a union so, at this stage we wont necessarily see unions.
Testing It
Next step
The output of this parser is passed on to the type matcher as described on the page here.