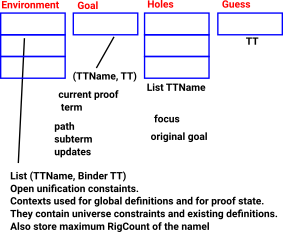
Proof State

Tactics operate on the proof state. The proof state contains various pieces of information, at this stage, the important ones for us are:
- holes - a stack of hole names.
- current goal - proof term
- original goal - proof type
- context
from David Christiansen paper:
- A goal type - the type of the term that is under construction.
- A possibly incomplete proof term, which should inhabit the goal type at the end of elaboration.
- A hole queue, tracking the incomplete portions of the proof term.
- A collection of open unification problems, representing recoverable failures of unification that may yet unify once more variables are solved.
- Various deferred operations, such as the bodies of case blocks that need to be elaborated.
There are many other pieces of information in the proof state such as the names used but, for now, we will leave the system to handle these.

Elaborator Reflection
The Idris part of the code for elaborator reflection is in
Idris-dev/libs/prelude/Language/Reflection/Elab.idr
Before we look at the Elab monad we need to know how to construct terms.
Names TTName
Names in an Idris program are evaluated at runtime but sometimes we need a 'variable name' which can be referred to as an unevaluated symbol.
The names used in terms have different constructors depending on their type:
| UN String | A user-provided name |
| NS (UN "foo") ["B", "A"]) | A name in some namespace |
| MN Int String | Machine-chosen names |
| SN SpecialName | Special names, to make conflicts impossible and language features predictable |
| A user defined name can be constructed like this: | Idris> UN "x" UN "x" : TTName |
Idris> NS (UN "x") ["b","a"] NS (UN "x") ["b", "a"] : TTName |
|
A machine-chosen name needs to be generated within an Elab monad (see below for details) and is unique within that monad:
This produced: {abc_140}{abc_141} So although gensym "abc" was called twice each one had a different integer.
|
implementation Show TTName where
show (UN s) = "`{{"++s++"}}"
show (NS t a) = "{"++(show t)++"."++(show a)++"}"
show (MN i s) = "{"++s++"_"++(show i)++"}"
show (SN sn) = "TTName special name"
showGensym : String
showGensym = %runElab (do
debugMessage [TextPart (
show !(gensym "abc") ++
show !(gensym "abc")
)]
) |
Quasiquotation
Since names are used frequently in elaborator reflection there is a shortcut for constructing them:
Idris> `{{x}}
UN "x" : TTName |
|
Idris> `{x}
No such variable x
Idris> :let x=2
Idris> `{x}
UN "x" : TTName |
|
Idris> :let a=2 Idris> `(a) P Ref (UN "a") (TConst (AType (ATInt ITBig))) : TT |
|
Idris> `(a:Integer) P Ref (UN "a") (TConst (AType (ATInt ITBig))) : TT |
|
Idris> `(~a) 2 : Integer |
quasiquotation summary:
| Reification | ||
| `{{n}} | TTName | Use for new names. Unresolved quotation of the name n. |
| `{n} | TTName | Use for existing names. Resolved quotation of the name n. n is a reference to a unique name in scope. |
| `(e) | expression e for which a type is inferable. | |
| `(e:t) | expression e with a given type e. | |
| ~a | anti-quotation - sub region which can be evaluated rather than quoted. | |
| (Var `{{x}}) | Raw |
TT:
There is a notation for a term in TT as it is being constructed (based on a BNF-like grammar), this is used for example in the debug output, it is a compact way to see the state of the term so we use it here.
So internally the program is stored as a tree structure using the following syntax:
| Syntax | More Information | ||
|---|---|---|---|
| term | t | ||
| binding | b | ||
| constant | t ::= | c | |
| variable | t ::= | x | |
| variable binding | t ::= | b.t | so a dot '.' tells us this is some sort of binding. |
| application | t ::= | t t | As with Idris, juxtaposition indicates function application. Note: we use the same symbol 't' for terms |
| Type constructor | t ::= | T | |
| Data constructor | t ::= | C | |
| function | b::= | λ c:t | colon ':' separates parameters from body of binding. |
| let binding | b::= | let |-> t:t | |
| function | b::= | ∀ x:t | |
| Type universe | c::= | *i | The universe hierarchy is usually handled automatically so we can just use * for the type of types. |
| integer literal | c:== | i | |
| integer type | c:== | Integer | |
| string literal | c:== | s | |
| string type | c:== | String | |
| focused hole | ?x : t | Conor McBride 1999 thesis. | |
| guess | ?x ≈ t : t | Conor McBride 1999 thesis. |
Sometimes the part of the term in focus is underlined.
||| Reflection of the well typed core language
data TT =
||| A reference to some name (P for Parameter)
P NameType TTName TT |
||| de Bruijn variables
V Int |
||| Bind a variable
Bind TTName (Binder TT) TT |
||| Apply one term to another
App TT TT |
||| Embed a constant
TConst Const |
||| Erased terms
Erased |
||| The type of types along (with universe constraints)
TType TTUExp |
||| Alternative universes for dealing with uniqueness
UType Universe |
TT stores local bound variables using De Bruijn index, when working in Idris this does not concern the user because string names are used for variables. Converting bound variables internally to index values means that the same variable name can be used, in different lambda terms, without ambiguity and without the need for α-substitution.
De Bruijn index which is a integer where:
- 0=inside current (inner) lambda term
- 1= next outer lambda term
- 2= next outer and so on
Expression Notation
The notation assumes right-associativity, in the absence of brackets, the term to the right binds more tightly than the one on the left .
so, for nested lambda terms:
λ a . λ b . f
means
λ a .( λ b . f)
and the same for function application:
f g x
means
f (g x)
In contrast, in lambda calculus, function application is usually regarded as left-associative,
Here are some typical examples of the notation used for expressions:
| Notation | Meaning |
|---|---|
? {hole_0} . {hole_0} |
The term, to be derived, may start off in this state following something like this: myScript : Elab () myScript= do The dot '.' tells us this is some sort of binding. |
?{hole_0} ≈ ? {hole_2} . {hole_2} . {hole_0} |
Here is a slightly more complicated example arising from: idNat : Nat -> Nat idNat = %runElab (do This introduces a guess that hole_0 = hole_2 . |
?{hole_0} ≈ λ x . ? {hole_2} . {hole_2} . {hole_0} |
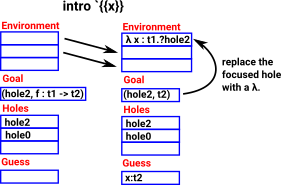
Following on from the previous example a lambda function is introduced like this: intro `{{x}}
So now the expression is wrapped in a lambda binding. |
?{hole_0} ≈ λ x . ?{hole_2} ≈ x . {hole_2} . {hole_0} |
Following on, we can use the fill tactic like this: fill (Var `{{x}})
which introduces another guess. |
?{hole_0} ≈ λ x . x . {hole_0} |
The solve tactic completes the proof |
Raw
data Raw =
||| Variables, global or local
Var TTName |
||| Bind a variable
RBind TTName (Binder Raw) Raw |
||| Application
RApp Raw Raw |
||| The type of types
RType |
||| Alternative universes for dealing with uniqueness
RUType Universe |
||| Embed a constant
RConstant Const |
Elab Tactics
||| A reflected elaboration script.
export
data Elab : Type -> Type where
-- obligatory control stuff
Prim__PureElab : a -> Elab a
Prim__BindElab : {a, b : Type} -> Elab a -> (a -> Elab b) -> Elab b
Prim__Try : {a : Type} -> Elab a -> Elab a -> Elab a
Prim__TryCatch : {a : Type} -> Elab a -> (Err -> Elab a) -> Elab a
Prim__Fail : {a : Type} -> List ErrorReportPart -> Elab a
Prim__Env : Elab (List (TTName, Binder TT))
Prim__Goal : Elab (TTName, TT)
Prim__Holes : Elab (List TTName)
Prim__Guess : Elab TT
Prim__LookupTy : TTName -> Elab (List (TTName, NameType, TT))
Prim__LookupDatatype : TTName -> Elab (List Datatype)
Prim__LookupFunDefn : TTName -> Elab (List (FunDefn TT))
Prim__LookupArgs : TTName -> Elab (List (TTName, List FunArg, Raw))
Prim__Check : List (TTName, Binder TT) -> Raw -> Elab (TT, TT)
Prim__SourceLocation : Elab SourceLocation
Prim__Namespace : Elab (List String)
Prim__Gensym : String -> Elab TTName
Prim__Solve : Elab ()
Prim__Fill : Raw -> Elab ()
Prim__Apply : Raw -> List Bool -> Elab (List (TTName, TTName))
Prim__MatchApply : Raw -> List Bool -> Elab (List (TTName, TTName))
Prim__Focus : TTName -> Elab ()
Prim__Unfocus : TTName -> Elab ()
Prim__Attack : Elab ()
Prim__Rewrite : Raw -> Elab ()
Prim__Claim : TTName -> Raw -> Elab ()
Prim__Intro : Maybe TTName -> Elab ()
Prim__Forall : TTName -> Raw -> Elab ()
Prim__PatVar : TTName -> Elab ()
Prim__PatBind : TTName -> Elab ()
Prim__LetBind : TTName -> Raw -> Raw -> Elab ()
Prim__Compute : Elab ()
Prim__Normalise : (List (TTName, Binder TT)) -> TT -> Elab TT
Prim__Whnf : TT -> Elab TT
Prim__Converts : (List (TTName, Binder TT)) -> TT -> TT -> Elab ()
Prim__DeclareType : TyDecl -> Elab ()
Prim__DefineFunction : FunDefn Raw -> Elab ()
Prim__DeclareDatatype : TyDecl -> Elab ()
Prim__DefineDatatype : DataDefn -> Elab ()
Prim__AddImplementation : TTName -> TTName -> Elab ()
Prim__IsTCName : TTName -> Elab Bool
Prim__ResolveTC : TTName -> Elab ()
Prim__Search : Int -> List TTName -> Elab ()
Prim__RecursiveElab : Raw -> Elab () -> Elab (TT, TT)
Prim__Fixity : String -> Elab Fixity
Prim__Debug : {a : Type} -> List ErrorReportPart -> Elab a
Prim__Metavar : TTName -> Elab ()
|
Here we look at each tactic in turn to see how they affect the proof state.
Binders
Introduction tactics for binders. The binder types are:
- lambda function (intro)
- dependent function (forall)
- let (letBind)
- pattern (patbind)
A precondition of these tactics is that the focused hole is of the form:
?h : t.h
that is, that the body of its scope consists directly of a reference to the hole-bound variable. If a hole binder were of the form:
?h : t1 -> t2.f h
and a tactic such as
intro `{{x}}
were applied, the result would be the term
?h : t2 . λ x:t1. f h
However this would cause the application of f to be ill-typed, as it expects an argument of type t1->t2, not an argument of type t2. Additionally, some binding tactics require that t, the type of the hole h, have a specific form, because the binder to be established may have a typing rule associated with it.
| intro |
Introduce a lambda binding around the current hole and focus on the body. Requires that the hole be in binding form (use 'attack' if it might not be). Signature: intro : (n : TTName) -> Elab () Result λn:t1.?h:[n/x]t2.h
|
| intro' | Introduce a lambda binding around the current hole and focus on the body, using the name provided by the type of the hole. Signature: intro' : Elab () |
| forall | Introduce a dependent function type binding into the current hole, and focus on the body. Signature: forall : TTName -> Raw -> Elab () |
| patbind | Introduce a new pattern binding. Signature: patbind : TTName -> Elab () |
| letbind | Introduce a new let binding. Signature: letbind : (n : TTName) -> (ty, tm : Raw) -> Elab () |
Primitive Operators
| gensym | Generate a unique name based on some hint. Useful when establishing a new binder. Signature: gensym : (hint : String) -> Elab TTName |
| solve | Substitute a guess into a hole. Substitute the focused guess throughout its scope, eliminating it and moving focus to the next element of the hole queue. Fail if the focus is not a guess. Signature: solve : Elab () |
| fill | Place a term into a hole, unifying its type. Fails if the focus is not a hole. Signature: fill : (e : Raw) -> Elab () Place a term e with type tc into the focused hole: ?h : th.e' and convert it to a guess: ?h ≈ e:t.e' and fail if the current focus is not a hole. The type t of the guess is constructed by unifying tc and th, which may instantiate holes that they refer to. Fail if the current focus is not a hole or if unification fails. This unification can result in the solution of further holes or the establishment of additional unsolved unification constraints. |
| apply | Attempt to apply an operator to fill the current hole, potentially solving arguments by unification. A hole is established for each argument. The return value is the list of holes established for the arguments to the function. Note that not all of the returned hole names still exist, as they may have been solved. Signature: apply : (op : Raw) -> (argSpec : List Bool) -> Elab (List TTName) Example: elaborating an application of a function f that takes one implicit and two explicit arguments might invoke: apply `(f) [False, True, True] Here is an example of an elab script that uses apply to insert the term plus Z (S Z) into a goal of type Nat. do [x,y] <- apply `(plus) [False, False] solve focus x; fill `(Z); solve focus y; fill `(S Z); solve The names of the established holes are returned. Note: This was added to the original tactic language to allow elaborator reflection. |
| matchApply | Attempt to apply an operator to fill the current hole, potentially solving arguments by matching. Signature: matchApply : (op : Raw) -> (argSpec : List Bool) ->
Elab (List TTName) |
| focus | Move the focus to the specified hole, bringing it to the front of the hole queue. Fails if the hole does not exist. Signature: focus : (hole : TTName) -> Elab () |
| unfocus | Send the currently-focused hole to the end of the hole queue and focus on the next hole. Signature: unfocus : TTName -> Elab () |
| attack | Convert a hole to make it suitable for bindings - that is, transform it such that it has the form `?h : t . h` as opposed to `?h : t . f h`. Signature: attack : Elab () |
| claim | Establish a new hole binding named n with type t, surrounding the current focus. Introduce a new hole with a specified name and type. Signature: claim : TTName -> Raw -> Elab () |
| patvar | Convert a hole into a pattern variable. Signature: patvar : TTName -> Elab () |
| compute | Normalise the goal. Often this is not necessary because normanisation is applied during other tactics. Signature: compute : Elab () |
| normalise | Normalise a term in some lexical environment Signature: normalise : (env : List (TTName, Binder TT)) ->
(term : TT) -> Elab TT |
| whnf | Reduce a closed term to weak-head normal form Signature: whnf : (term : TT) -> Elab TT |
| convertsInEnv | Check that two terms are convertible in the current context and in some environment. Signature: convertsInEnv : (env : List (TTName, Binder TT)) ->
(term1, term2 : TT) -> Elab () |
| converts | Check that two terms are convertable in the current context and environment converts : (term1, term2 : TT) -> Elab ()
converts term1 term2 = convertsInEnv !getEnv term1 term2
|
| getSourceLocation | Find the source context for the elaboration script Signature: getSourceLocation : Elab SourceLocation |
| sourceLocation | Attempt to solve the current goal with the source code location sourceLocation : Elab ()
sourceLocation = do loc <- getSourceLocation
fill (quote loc)
solve
|
| currentNamespace | Get the current namespace at the point of tactic execution. This allows scripts to define top-level names conveniently. Signature: currentNamespace : Elab (List String) |
| rewriteWith | Attempt to rewrite the goal using an equality. Signature: rewriteWith : Raw -> Elab () |
| resolveTC | Attempt to solve the current goal with an interface dictionary Signature: resolveTC : (fn : TTName) -> Elab () |
| search | Use Idris's internal proof search. Signature: search : Elab () |
| search' | Use Idris's internal proof search, with more control. Signature: search' : (depth : Int) -> (hints : List TTName) -> Elab () |
| operatorFixity | Look up the declared fixity for an operator. Signature: operatorFixity : (operator : String) -> Elab Fixity |
| debug | Halt elaboration, dumping the internal state for inspection. Signature: debug : Elab a Only seems to compile if 'debug' is last tactic so comment out following tactics like this: %language ElabReflection
idNat : Nat -> Nat
idNat = %runElab (do
intro `{{x}}
debug
-- fill (Var `{{x}})
-- solve
) |
| debugMessage | Halt elaboration, dumping the internal state and displaying a message. Signature: debugMessage : (msg : List ErrorReportPart) -> Elab a Only seems to compile if 'debug' is last tactic so comment out following tactics like this: %language ElabReflection idNat : Nat -> Nat
idNat = %runElab (do
intro `{{x}}
debugMessage [TextPart "error message"]
-- fill (Var `{{x}})
-- solve
) |
| metavar | Create a new top-level metavariable to solve the current hole. Signature: metavar : (name : TTName) -> Elab () |
| runElab | Recursively invoke the reflected elaborator with some goal. Signature: runElab : Raw -> Elab () -> Elab (TT, TT) |
Read and Write State
| getEnv | Look up the lexical binding at the focused hole. Fails if no holes are present. Signature: getEnv : Elab (List (TTName, Binder TT)) returns the type: Elab (List (TTName, Binder TT)) |
| getGoal | Get the name and type of the focused hole. Fails if not holes are present. Signature: getGoal : Elab (TTName, TT) |
| getHoles | Get the hole queue, in order. getHoles : Elab (List TTName) getHoles = Prim__Holes |
| getGuess | If the current hole contains a guess, return it. Otherwise, fail. getGuess : Elab TT getGuess = Prim__Guess |
| lookupTy | Look up the types of every overloading of a name. lookupTy : TTName -> Elab (List (TTName, NameType, TT)) lookupTy n = Prim__LookupTy n |
| lookupTyExact | Get the type of a fully-qualified name. Fail if it doesn't resolve uniquely. lookupTyExact : TTName -> Elab (TTName, NameType, TT)
lookupTyExact n = case !(lookupTy n) of
[res] => pure res
[] => fail [NamePart n, TextPart "is not defined."]
xs => fail [NamePart n, TextPart "is ambiguous."] |
| lookupDatatype | Find the reflected representation of all datatypes whose names are overloadings of some name. lookupDatatype : TTName -> Elab (List Datatype) lookupDatatype n = Prim__LookupDatatype n |
| lookupDatatypeExact | Find the reflected representation of a datatype, given its fully-qualified name. Fail if the name does not uniquely resolve to a datatype. lookupDatatypeExact : TTName -> Elab Datatype
lookupDatatypeExact n = case !(lookupDatatype n) of
[res] => pure res
[] => fail [TextPart
"No datatype named", NamePart n]
xs => fail [TextPart "More than one datatype named",
NamePart n] |
| lookupFunDefn | Find the reflected function definition of all functions whose names are overloadings of some name. lookupFunDefn : TTName -> Elab (List (FunDefn TT)) lookupFunDefn n = Prim__LookupFunDefn n |
| lookupFunDefnExact | Find the reflected function definition of a function, given its fully-qualified name. Fail if the name does not uniquely resolve to a function. lookupFunDefnExact : TTName -> Elab (FunDefn TT)
lookupFunDefnExact n = case !(lookupFunDefn n) of
[res] => pure res
[] => fail [TextPart
"No function named", NamePart n]
xs => fail [TextPart "More than one function named",
NamePart n] |
| lookupArgs | Get the argument specification for each overloading of a name. lookupArgs : TTName -> Elab (List (TTName, List FunArg, Raw)) lookupArgs n = Prim__LookupArgs n |
| lookupArgsExact | Get the argument specification for a name. Fail if the name does not uniquely resolve. lookupArgsExact : TTName -> Elab (TTName, List FunArg, Raw)
lookupArgsExact n = case !(lookupArgs n) of
[res] => pure res
[] => fail [NamePart n, TextPart "is not defined."]
xs => fail [NamePart n, TextPart "is ambiguous."] |
| check | Attempt to type-check a term, getting back itself and its type. check : (env : List (TTName, Binder TT)) ->
(tm : Raw) -> Elab (TT, TT)
check env tm = Prim__Check env tm
|
Error Handling
| tryCatch | `tryCatch t (\err => t')` will run `t`, and if it fails, roll back the elaboration state and run `t'`, but with access to the knowledge of why `t` failed. Signature: tryCatch : Elab a -> (Err -> Elab a) -> Elab a Fixme - following does not work. %language ElabReflection
id1 : Elab ()
id1 = do
tryCatch (intro `{{x}})
(\err -> (intro `{{x}}))
fill (Var `{{x}})
solve
idNat : Nat -> Nat
idNat = %runElab id1 |
| fail | Halt elaboration with an error Signature: fail : List ErrorReportPart -> Elab a Return type is given by last term so fail cant be at the the last term, we would expect fail to be in some sort of conditional statement: %language ElabReflection
id1 : Elab ()
id1 = do
intro `{{x}}
fill (Var `{{x}})
if True
then
fail [TextPart "error message"]
else
solve
idNat : Nat -> Nat
idNat = %runElab id1 |
Generating Data and Functions at Compile Time
We can construct a data structure at compile-time in an Elab monad.
This can allow proofs to be generated for user defined types or it could allow types to be automatically generated to support user defined types.
An example is the code, from Christensen-Brady joint paper ('Elaborator Reflection: Extending Idris in Idris'), that automatically generates accessibility predicates using the Bove-Capretta method.
The following simple outline example is adapted from https://github.com/idris-lang/Idris-dev/blob/master/test/meta002/DataDef.idr
module DataDef
%language ElabReflection
addData : Elab ()
addData = do
let dataname : TTName = `{{DataDef.N}}
declareDatatype $ Declare dataname [MkFunArg `{{n}} `(Nat) Explicit NotErased] `(Type)
defineDatatype $ DefineDatatype dataname [
Constructor `{{MkN}} [MkFunArg `{{x}} `(Nat) Implicit NotErased]
(RApp (Var `{{DataDef.N}}) (Var `{{x}})),
Constructor `{{MkN'}} [MkFunArg `{{x}} `(Nat) Explicit NotErased]
(RApp (Var `{{DataDef.N}}) (RApp (Var `{S}) (Var `{{x}})))
]
%runElab addData
|
So this declares and defines the following data structure 'N' with a constructor 'MkN' which can have an implicit or an explicit Nat argument. data N : Nat -> Type where MkN : N x MkN' : (x : Nat) -> N (S x) |
λΠ> :t N N : Nat -> Type λΠ> N 2 N 2 : Type λΠ> N 0 N 0 : Type λΠ> :t MkN MkN : N x |
Here is another, more complicated, example from the same test file. This also creates a function.
module DataDef
%language ElabReflection
mkU : Elab ()
mkU = do
let U = `{{DataDef.U}}
let el = `{{DataDef.el}}
declareDatatype $ Declare U [] `(Type)
declareType $ Declare el [MkFunArg `{{code}} (Var U) Explicit NotErased] `(Type)
defineDatatype $ DefineDatatype U [
Constructor `{{Base}} [] (Var U),
Constructor `{{Pi}}
[MkFunArg `{{code}} (Var U) Explicit NotErased,
MkFunArg `{{body}} `(~(RApp (Var el) (Var `{{code}})) -> ~(Var U)) Explicit NotErased]
(Var U)
]
defineFunction $ DefineFun el [
MkFunClause (RBind `{{code}} (PVar (Var U))
(RBind `{{body}} (PVar `(~(RApp (Var el) (Var `{{code}})) -> ~(Var U)))
(RApp (Var el)
(RApp (RApp (Var `{{DataDef.Pi}})
(Var `{{code}}))
(Var `{{body}})))))
(RBind `{{code}} (PVar (Var U))
(RBind `{{body}} (PVar `(~(RApp (Var el) (Var `{{code}})) -> ~(Var U)))
(RBind `{{x}} (Pi (RApp (Var el) (Var `{{code}})) `(Type))
(RApp (Var el) (RApp (Var `{{body}}) (Var `{{x}})))))),
MkFunClause (RApp (Var el) (Var `{{DataDef.Base}})) `(Bool)
]
%runElab mkU
|
This code generates the following data and function
data U : Type where Base : U Pi : (code : U) -> (el code -> U) -> U el : U -> Type el (Pi code body) = (x : el code) -> el (body x) el Base = Bool |
λΠ> :t U U : Type λΠ> :doc U No documentation for U λΠ> Base Base : U λΠ> DataDef.Pi Pi : (code : U) -> (el code -> U) -> U λΠ> |
λΠ> :t el el : U -> Type λΠ> el Base Bool : Type |
So these are the functions that we can use to create data and functions in the Elab monad:
| declareType | Add a type declaration to the global context. Signature: declareType : TyDecl -> Elab () |
| defineFunction | Define a function in the global context. The function must have already been declared, either in ordinary Idris code or using `declareType`. Signature: defineFunction : FunDefn Raw -> Elab () |
| declareDatatype | Declare a datatype in the global context. This step only establishes the type constructor; use `defineDatatype` to give it constructors. Signature: declareDatatype : TyDecl -> Elab () |
| defineDatatype | Signature: defineDatatype : DataDefn -> Elab () |
| addImplementation | Register a new implementation for interface resolution. Signature: addImplementation : (ifaceName, implName : TTName) -> Elab () |
| isTCName | Determine whether a name denotes an interface. Signature: isTCName : (name : TTName) -> Elab Bool |
The above functions use the following data/records:
Plicity How an argument is provided in high-level Idris |
data Plicity= ||| The argument is directly provided at the application site Explicit | ||| The argument is found by Idris at the application site Implicit | ||| The argument is solved using interface resolution Constraint |
FunArg Function arguments - These are the simplest representation of argument lists, and are used for functions. Additionally, because a FunArg provides enough information to build an application, a generic type lookup of a top-level identifier will return its FunArgs, if applicable. |
record FunArg where constructor MkFunArg name : TTName type : Raw plicity : Plicity erasure : Erasure |
TyConArg Type constructor arguments Each argument is identified as being either a parameter that is consistent in all constructors, or an index that varies based on which constructor is selected. |
data TyConArg = ||| Parameters are uniform across the constructors TyConParameter FunArg | ||| Indices are not uniform TyConIndex FunArg |
TyDecl A type declaration for a function or datatype |
record TyDecl where constructor Declare ||| The fully-qualified name of the function or datatype being declared. name : TTName ||| Each argument is in the scope of the names of previous arguments. arguments : List FunArg ||| The return type is in the scope of all the argument names. returnType : Raw |
FunClause A single pattern-matching clause |
data FunClause : Type -> Type where MkFunClause : (lhs, rhs : a) -> FunClause a MkImpossibleClause : (lhs : a) -> FunClause a |
FunDefn A reflected function definition. |
record FunDefn a where constructor DefineFun name : TTName clauses : List (FunClause a) |
ConstructorDefn A constructor to be associated with a new datatype. |
record ConstructorDefn where constructor Constructor ||| The name of the constructor. The name must _not_ be qualified - ||| that is, it should begin with the `UN` or `MN` constructors. name : TTName ||| The constructor arguments. Idris will infer which arguments are ||| datatype parameters. arguments : List FunArg ||| The specific type constructed by the constructor. returnType : Raw |
DataDefn A definition of a datatype to be added during an elaboration script. |
record DataDefn where constructor DefineDatatype ||| The name of the datatype being defined. It must be ||| fully-qualified, and it must have been previously declared as a ||| datatype. name : TTName |
| CtorArg | data CtorArg = CtorParameter FunArg | CtorField FunArg |
Datatype A reflected datatype definition |
record Datatype where constructor MkDatatype ||| The name of the type constructor name : TTName ||| The arguments to the type constructor tyConArgs : List TyConArg ||| The result of the type constructor tyConRes : Raw ||| The constructors for the family constructors : List (TTName, List CtorArg, Raw) |