I can think of two methods to derive the equations:
- Invert Axis-Angle to Matrix equations
- Convert Axis-Angle to quaternion then convert to Matrix
I have both of these on this page, I think inverting the Axis-Angle to Matrix equations is the most useful so lets try that first:
Method 1 - Invert Axis-Angle to Matrix equations
On the axis-angle to matrix page we saw that an axis-angle rotation can be written as the sum of 3 matricies:
- The identity matrix times c.
- A matrix which is symmetrical about the leading diagonal.
- A matrix which is antisymmetrical about the leading diagonal (term on other side of diagonal is negative).
| t*x*x + c |
t*x*y - z*s |
t*x*z + y*s |
| t*x*y + z*s |
t*y*y + c |
t*y*z - x*s |
| t*x*z - y*s |
t*y*z + x*s |
t*z*z + c |
|
= c* |
|
+ t* |
| x*x |
x*y |
x*z |
| x*y |
y*y |
y*z |
| x*z |
y*z |
z*z |
|
+s* |
|
In this case we are starting with a matrix. We can divide this matrix into symmetrical and antisymmetrical components as follows:
| m00 |
m01 |
m02 |
| m10 |
m11 |
m12 |
| m20 |
m21 |
m22 |
|
= |
| m00 |
(m01+m10)/2 |
(m02+m20)/2 |
| (m10+m01)/2 |
m11 |
(m12+m21)/2 |
| (m20+m02)/2 |
(m21+m12)/2 |
m22 |
|
+ |
| 0 |
(m01-m10)/2 |
(m02-m20)/2 |
| (m10-m01)/2 |
0 |
(m12-m21)/2 |
| (m20-m02)/2 |
(m21-m12)/2 |
0 |
|
If we equate the antisymmetrical components in the above two equations we get:
s * x = (m21-m12)/2
s * y = (m02-m20)/2
s * z = (m10-m01)/2
where,
- c =cos(angle)
- s = sin(angle)
- t =1 - c
- x = normalised axis x coordinate
- y = normalised axis y coordinate
- z = normalised axis z coordinate
If we equate the symmetrical components in the above two equations we get:
t * x*y = (m10+m01)/2
t * x*z = (m20+m02)/2
t * y*z = (m21+m12)/2
Deriving the Angle
If we equate the terms on the leading diagonal we get:
t*x*x + c = m00
t*y*y + c = m11
t*z*z + c = m22
Adding these last 3 equations gives:
t*x*x + c + t*y*y + c + t*z*z + c = m00 + m11 + m22
t*(x*x + y*y + z*z) +3*c = m00 + m11 + m22
but since the axis is normalised x*x + y*y + z*z = 1 so,
t+3*c = m00 + m11 + m22
substituting t =1 - c gives,
(1 - c)+3*c = m00 + m11 + m22
1 + 2*c = m00 + m11 + m22
c = (m00 + m11 + m22 - 1)/2
therefore:
angle = acos((m00 + m11 + m22 - 1)/2)
Deriving the axis
squaring the above equation we get:
c2 = (m00 + m11 + m22 - 1)2/4
but,
-s2 = c2 - 1
-s2 = (m00 + m11 + m22 - 1)2/4 - 1
We now take the square root of both sides of the equation, this is a worrying operation both because it allows the possibility of a positive or a negative solution and the possibility of a complex solution over part of the range. It is tempting to try to find a method which does not involve square roots, however I don't think we are going to find that because there are two solutions, an axis in one direction with a positive angle, or an axis in the other direction with an equal and opposite angle.
s = ±sqrt((m00 + m11 + m22 - 1)2/4 - 1)
Substituting this in the equations derived from the antisymmetrical components we get:
s * x = (m21-m12)/2
s * y = (m02-m20)/2
s * z = (m10-m01)/2
so,
x = (m21-m12)/(2*sqrt((m00 + m11 + m22 - 1)2/4 - 1))
y = (m02-m20)/(2*sqrt((m00 + m11 + m22 - 1)2/4 - 1))
z = (m10-m01)/(2*sqrt((m00 + m11 + m22 - 1)2/4 - 1))
Method 2 - convert Axis-Angle to quaternion then convert to Matrix
To calculate first convert to quaternion as explained here:
qw = sqrt(1.0 + m00 + m11 + m22) / 2.0
qx = (m21 - m12) / (4.0 * qw)
qy = (m02 - m20) / (4.0 * qw)
qz = (m10 - m01) / (4.0 * qw)
Than convert quaternion value to axis angle as explained here
angle = 2 * acos(qw)
x = qx / sqrt(1-qw*qw)
y = qy / sqrt(1-qw*qw)
z = qz / sqrt(1-qw*qw)
The axis values x,y and z can be multiplied by a common factor without altering
the direction of the axis (we will re-normalise it to unit length later).
angle = 2 * acos(sqrt(1.0 + m00 + m11 + m22) / 2.0)
x = m21 - m12
y = m02 - m20
z = m10 - m01
to normalise the axis to unit length we need to divide x,y and z by:
sqrt(x2+y2+z2)
=sqrt(m21 - m12)2+(m02 - m20)2+(m10 - m01)2 )
so normalised value is:
angle = 2 * acos(sqrt(1.0 + m00 + m11 + m22) / 2.0)
x = (m21 - m12)/sqrt((m21 - m12)2+(m02 - m20)2+(m10 -
m01)2)
y = (m02 - m20)/sqrt((m21 - m12)2+(m02 - m20)2+(m10 -
m01)2)
z = (m10 - m01)/sqrt((m21 - m12)2+(m02 - m20)2+(m10 -
m01)2)
We can eliminate a sqrt function in the angle formula by using the double
angle formula.
if we let a=1.0 + m00 + m11 + m22
then we have angle = 2 * acos(sqrt(a) / 2)
rearranging gives: sqrt(a) / 2 = cos(angle/2)
squaring both sides gives: a / 4 = cos2(angle/2)
but the double angle formula gives: cos(angle) = 2 * cos2(angle/2) - 1
so cos(angle) = ( a / 2) - 1
angle = acos ( a/2 - 1 )
substituting the original formula for 'a' gives:
angle = acos ( (1.0 + m00 + m11 + m22)/2 - 1 )
angle = acos ( ( m00 + m11 + m22 - 1)/2)
|
So the final formula is as follows:
angle = acos ( ( m00 + m11 + m22 - 1)/2)
x = (m21 - m12)/sqrt((m21 - m12)2+(m02 - m20)2+(m10 -
m01)2)
y = (m02 - m20)/sqrt((m21 - m12)2+(m02 - m20)2+(m10 -
m01)2)
z = (m10 - m01)/sqrt((m21 - m12)2+(m02 - m20)2+(m10 -
m01)2)
It seems to me that with axis-angle there are always many ways to represent
the rotation, we can go the short way round (which will be an angle between
-pi and +pi) or we can go the long way round (which will be an angle between
+-pi and +-2pi) or multiples of 2pi of these. I guess in most cases we want
to find the shortest rotation arc.
In matrix notation there does not seem to be this distinction, so I guess the
conversion from matrix to axis-angle is one to many, but there is a one-to-one
relationship between matrix and shortest axis angle? We will get this if we
choose in acos implementation that returns angles angle between -pi and +pi?
I had a look at the documentation for both the java and C# Math libraries and
they both produce results in the following ranges:
asin input: -1 < n < 1 output: -pi/2 < n < pi/2
acos input: -1 < n < 1 output: 0 < n < pi
atan input: -inf< n < inf output: -pi/2 < n < pi/2
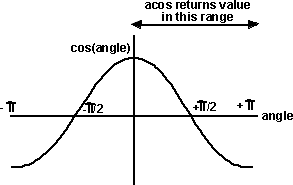
So in some cases we need to invert the angle, although inverting the axis will
produce the same result. If the angle and the axis are both inverted this will
produce the same rotation. (a similar issue is discussed with quaternions, ie
(w,x,y,z) and (-w,-x,-y,-z) both represent the same rotation).
So it is not clear if the above formula will work as required and invert the
axis when the angle is negative, However the following examples give me some
confidence that the formula above work as required.
For a discussion of this issue see these message from Sven.
Handling a de-orthogonalised Matrix
The above formulae don't use all the elements of the matrix, this is fine because an orthogonal rotation matrix contains a lot of redundant information. However, if we have already done a lot of transformations is possible that a lot of small floating point rounding errors could buld up, it may help minimise this if we use all the elements of the matrix in the hope of using the redundancy to cancel out, or at least, dilute the errors. One possible way to do this might be to re-orthogonalise the matrix first (as described here) and then apply the above formulae. However this is a bit messy and the following may provide a way to do the matrix to axis-angle conversion using more parameters.
This site may have errors. Don't use for critical systems.


