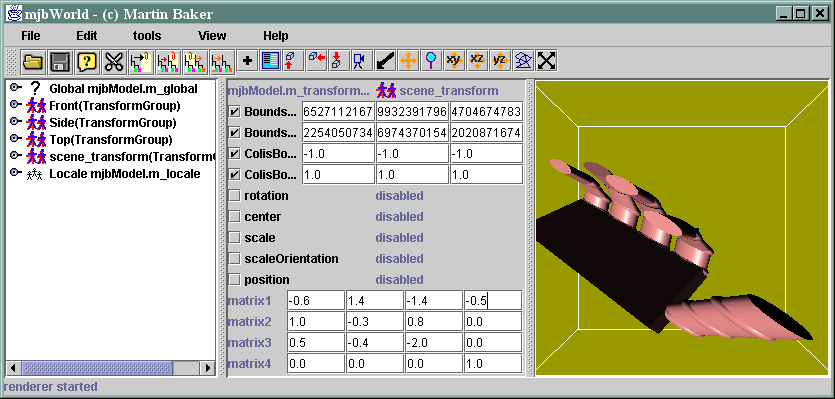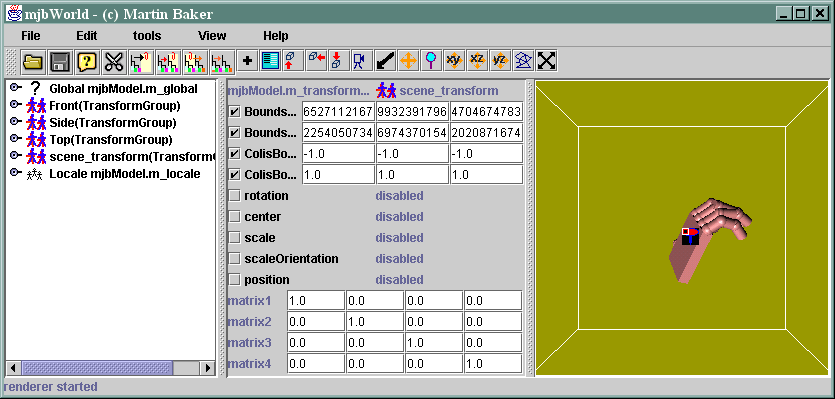
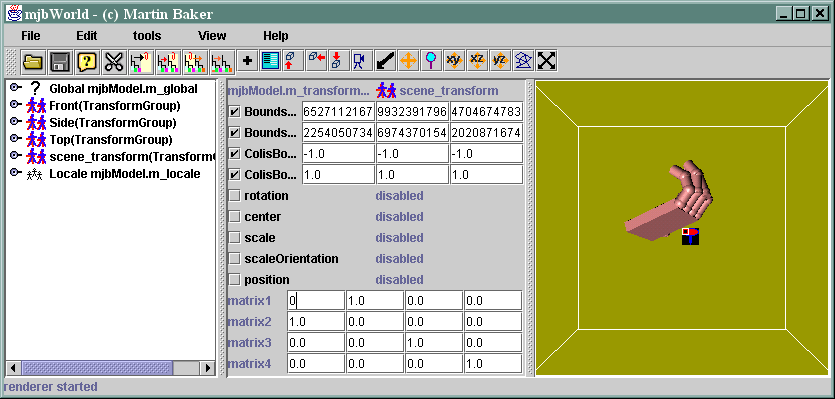
Select the transform node called scene_transform.
A TransformGroup node can have a number of nodes underneath it. It allows these nodes to be moved, rotated, scaled, etc. This can all be done by setting the values in the 4 by 4 matrix.
By default the matrix at the bottom of the parameters window shows the following values:
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
This is the do nothing matrix.
The matrix acts on all the vertexes in the nodes below the transformGroup
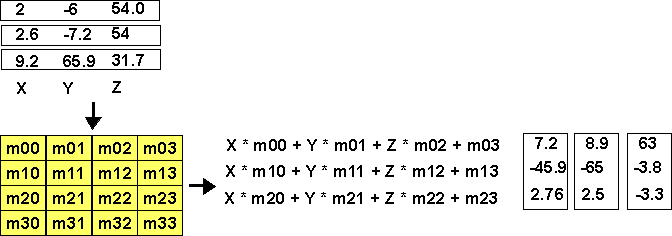
I tend to think of it as feeding in all the vertices from above, the values get multiplied by the corresponding values in the matrix, producing a new position for each vertex. This is what gives 3D programs a lot of power, you can rotate, translate, scale, etc. 3 dimentional objects just by applying a matrix to all the vertexes. It requires a lot of floating point multiplication's an additions, but the program to do this is very simple.
So lets see what happens when we try changing some values in the matrix.
If we change m11 from 1.0 to -1.0, this should invert the y (i.e. height) value which turns it upside down:
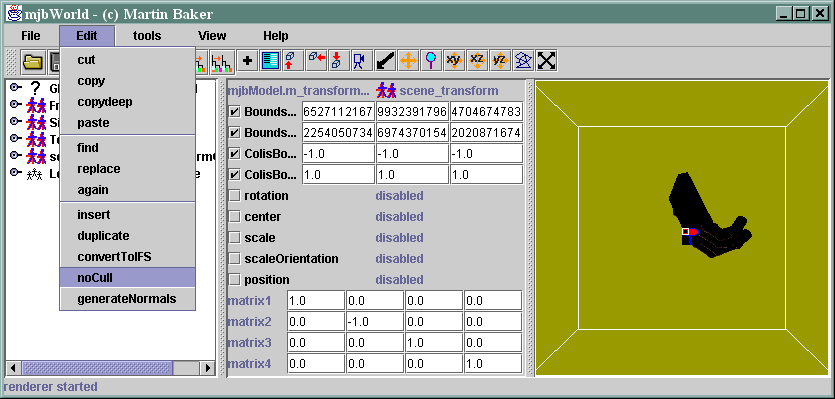
So what has happened here? Its turned it upside down, but its gone completely black This is because of the backface culling, to turn this off we need to set 'no culling' in the polygon attributes for every shape. mjbWorld provides a quick way to do this, just set noCull in the Edit menu.
Now it appears upside down as expected:
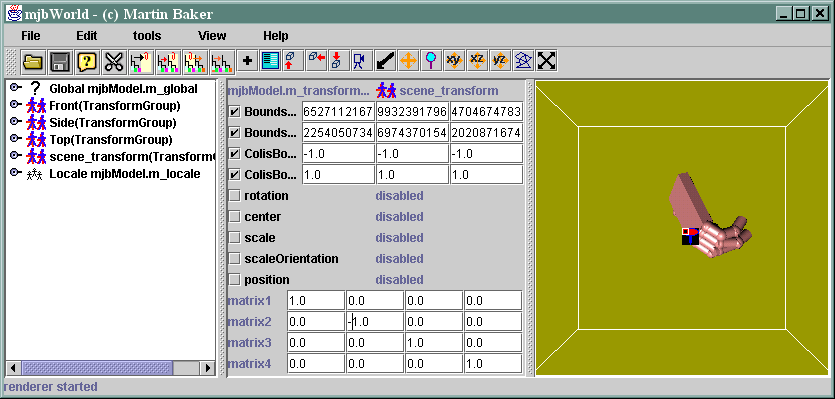
Lets try some other changes:
Setting the Z value to -1 inverts the depth, i.e. we see the back:
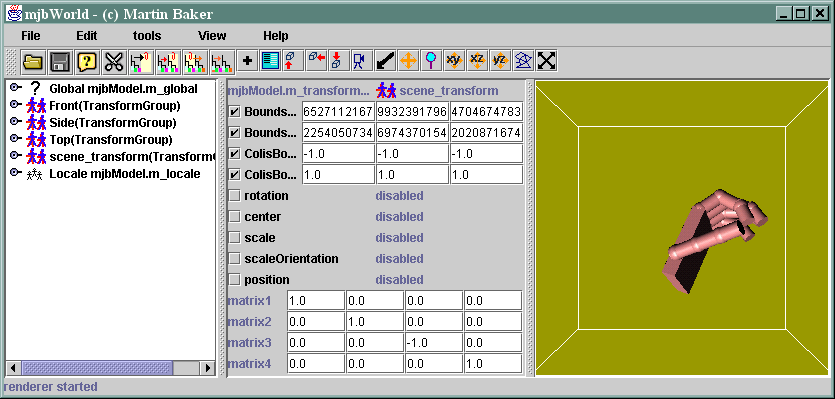
Why do we need a 4 by 4 matrix when we are only feeding 3 dimensional vectors through it? The right hand column shifts (or translates) the vertexes in the X,Y and Z directions.
If you enter not zero number in the right hand column you shift the position, for example the following moves the man left by 0.6 and down by 0.4
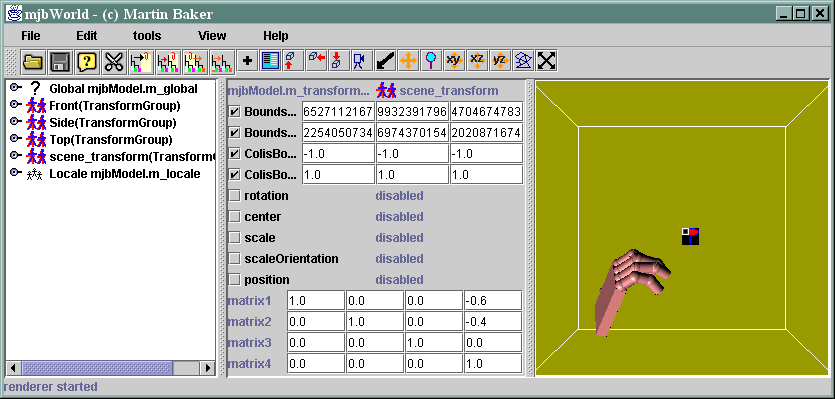
setting the matrix as follows:
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
This swaps the X and Y coordinates i.e. it rotates it by 90 degrees:
not all matrixes correspond to rotations, if you really want to torture this hand try entering a few random numbers into the matrix