When simulating solid 3D objects we need a way to specify, store and calculate the orientation and subsequent rotations of the object. I think of orientation as the current angular position of an object and rotation as an operation which takes a starting orientation and turns it into a possibly different orientation. However both rotation and orientation can be defined in the same way, provided we have a reference orientation we can always define orientation as a rotation from its reference orientation.
Rotational quantities are more difficult to represent than linear quantities, one method of holding this information is not suitable for all needs, therefore there are different ways to specify and perform this rotation, these methods include:
- Rotation about origin (orthogonal transformation)
- Representing Rotation with Translation (isometry).
- Angle between vectors
These means of specifying rotations have different pros and cons. We need to do things like, working out the effect of 2 or more subsequent rotations, also, in keyframing, we may want to generate in-between frames so we need to interpolate the rotations into smaller steps.
Notations like euler angles and Axis and Angle are intuitive easy to understand, but there are problems:
- When an object is rotating it suddenly jumps from 360 degrees back to zero.
- The 'gimbal lock' problem, there are singularities at certain points in the space where the normal rules don't apply.
- When applying one rotation and then applying another rotation, it is not valid to say that the total rotation is the sum of the individual rotations, therefore Axis and Angle is not a very good notation to use when combining rotations.
Quaternion arithmetic can represent operations in 3D space in a similar way that complex number arithmetic represents operations in 2D space. So quaternion arithmetic can be used to interpolate rotations in keyframe animation, without the instabilities associated with the previous notations.
Matrices have the advantage of defining both rotations and translations (i.e. linear and angular motion) so they can be used for things like kinematics where we need to do both, and we don't want to keep transferring between notations.
For more information about these different notation methods, click on the links below:
| number of parameters | concatenate rotations by multiplication | extend to model isometries | |
| Axis and angle | 4 | no | no |
| Euler angles | 3 | no | no |
| Quaternions | 4 | yes | dual quaternions |
| 3x3 Matrices | 9 | yes | 4x4 Matrices (16 parameters) |
| Multivectors | 8 | yes | yes |
There are also things to take into account when implementing rotations such as:
You can specify the position of a point using polar coordinates, this is covered separately from the topic of rotations.
Representing rotation using bivectors
Rotations in two dimensions are relatively easy, we can represent the rotation angle by a single scalar quantity, rotations can be combined by adding and subtracting the angles.
Rotations in a higher number of dimensions get more complicated. Any rotation can be represented by projecting the object onto a 2-dimentional plane and then rotating it through an angle. The plane can be defined by a bivector (see directed area box on right of this page). A bivector is the result of multiplying two vectors, the following table shows the dimension of the bivector produced by the multiplication of vectors of a given dimensions.
| vector dimensions | bivector dimensions |
|---|---|
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
The dimension of the bivector also gives the degree of freedom of rotations in the given dimension. For more information about rotations in higher dimensions see this page.
It just happens that in 3 dimensional vector space that bivectors also have three dimensions and therefore 3D rotations have 3 degrees of freedom.
We must be careful when combining rotations which are in a different plane, in this case we cannot combine them by adding the bivectors, we need other notations to do this.
For instance, in the case of linear translations, I could move an object up by 3 units (represented by [0,3,0]) and then move the object to the right by 4 units (represented by [4,0,0]). This would result in a position of [4,3,0], just simple vector addition. The order that I do these operations is not important, [0,3,0]+[4,0,0] = [4,0,0] + [0,3,0]. In neither case does this produce a component in the z dimension. However, in the rotational case we cannot make these assumptions, we cant find the result of applying subsequent rotations by just adding vectors and order of applying the rotations is important, we have to use different types of algebra such as matrices and quaternions to work out the effect of combining rotations.
Vectors like this are useful for representing some types of rotational quantities. This is because as the angles get smaller then combining rotations begins to approximate vector addition. So for angular velocities (w=da/dt) vector addition can be used, however we need to be very careful (for example rotational effects such as the procession of a gyroscope). This type of mathematics will be useful later for dynamics, for instance when we are dealing with torque, inertia etc.
Rotation in 2 dimensions
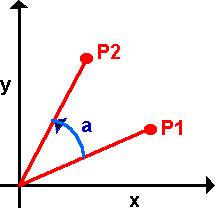
In order to investigate the issues, consider the simpler case of rotations in 2 dimensions. In 2 dimensions there is one degree of freedom, in 3 dimensions there are 3 degrees of freedom. How many degrees of freedom in 4D?
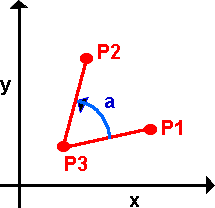
The above diagram shows the simple case of rotation about the origin, if we want to rotate about an arbitrary point P3, then one way to do this might be to subtract P3 from all points, then rotate about the origin, then add P3 to all points.
Rotations in 3D
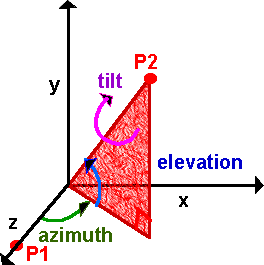
In 3D there are 3 degrees of freedom. Shown here as 3 angles, azimuth, elevation, and tilt. For example, if you were aiming a gun you would raise the barrel by a certain angle (elevation). Turn it in the direction required (azimuth). And if the barrel has rifled then the projectile will spin about its axis (tilt). In other areas, say nautical, different terms may be used such as roll, pitch and yaw.
Combining Rotations
If we rotate an object, then we do a second rotation on the object, we can calculate a single rotation which has the same effect of these two rotations. As said earlier, combining rotations in this way is most practically done using matrices or quaternions, because in these cases, the total rotation can be calculated by multiplying together the representation of the individual rotations. Note that order of operands is important and its important to use consistent definitions, for a discussion of how we might do this see this page, also see the pages for matrices and quaternions.
For a more theoretical mathematical approach to rotation read the group theory pages, but if you are interested in the more practical aspects of using and modeling rotations, the main principles are explained here.
Principles
- Two subsequent rotations can always be combined into a single rotation (see axis-angle).
- Order of applying rotations is important. Rotation A then Rotation B may give a different final orientation than applying Rotation B then Rotation A.
- There are many mathematical notations that can be used to represent rotations, but these principles always apply whatever notation is used.
- There is a do nothing rotation, for example, in the case of a matrix, this can be represented by the identity matrix.
- Three subsequent rotations can be combined in pairs either
(a * b) * c
or
a * (b * c)
will give the same result (as long as we don't change the order).
For 3D rotations there are 3 degrees of freedom, that is, any rotation can be defined with a minimum of 3 scalar inputs (but, as explained, we may choose to use more) One example might be:
- rotation about x axis
- rotation about y axis
- rotation about z axis
Affine Transformations
So far we are assuming that the rotations are about the origin of the co-ordinate system. If we want to rotate about any arbitrary point then we need to use a notation which can express both rotation and translation. This is covered here:

