Maths - Conversion Quaternion to Matrix

Equations

Quaternion multiplication and orthogonal matrix multiplication can both be used to represent rotation. If a quaternion is represented by qw + i qx + j qy + k qz , then the equivalent matrix, to represent the same rotation, is:

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

This page discusses the equivalence of quaternion multiplication and orthogonal matrix multiplication.

Alternative Method 1 - Product of two 4×4 matrices

Jay Ryness has kindly sent me this alternative method which calculates the result as a Product of two 4×4 matrices:

q.w q.z -q.y q.x
-q.z q.w q.x q.y
q.y -q.x q.w q.z
-q.x -q.y -q.z q.w
q.w q.z -q.y -q.x
-q.z q.w q.x -q.y
q.y -q.x q.w -q.z
q.x q.y q.z q.w

We are not sure exactly why this should be so, we would welcome any contribution to the discussion here.

Alternative Method 2 - Sum of three 3×3 matrices

The first matrix above can be written as the sum of three matrices:

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2
=
1 0 0
0 1 0
0 0 1
+2*
- qy2-qz2 qx*qy qx*qz
qx*qy - qx2-qz2 qy*qz
qx*qz qy*qz -qx2-qy2
+2*qw*
0 -qz qy
qz 0 -qx
-qy qx 0

I'm not sure if dividing the matrix up in this way has any use? But it seems to have a pattern and its interesting that the last part is a skew symmetric matrix usually associated with a vector 'cross' multiplication?

Issues

This assumes that the quaternion is normalised (sqw + sqx + sqy + sqz =1), if not it should be normalised before doing the conversion . To normalise divide qx, qy, qz and qw by n where n=sqrt(qx2 + qy2 + qz2 + qw2). See quaternion page for code.

Hamouras has pointed out, here, that the terms in the above matrix all involve the product of two terms (the '1' term is derives assuming a normalised quaternion), therefore if we delay the normaisation until we have calculated these pruducts we can avoid the square root.

The code below uses this method, if we are sure that the quaternion is already normalised we can leave out the invs terms.

This page assumes that we are using the standards defined on this page, for instance, the matrix is represented as following,

m00 m01 m02
m10 m11 m12
m20 m21 m22

Code

Java code to do conversion

public final void quatToMatrix(Quat4d q){
    double sqw = q.w*q.w;
    double sqx = q.x*q.x;
    double sqy = q.y*q.y;
    double sqz = q.z*q.z;

    // invs (inverse square length) is only required if quaternion is not already normalised
    double invs = 1 / (sqx + sqy + sqz + sqw)
    m00 = ( sqx - sqy - sqz + sqw)*invs ; // since sqw + sqx + sqy + sqz =1/invs*invs
    m11 = (-sqx + sqy - sqz + sqw)*invs ;
    m22 = (-sqx - sqy + sqz + sqw)*invs ;
    
    double tmp1 = q.x*q.y;
    double tmp2 = q.z*q.w;
    m10 = 2.0 * (tmp1 + tmp2)*invs ;
    m01 = 2.0 * (tmp1 - tmp2)*invs ;
    
    tmp1 = q.x*q.z;
    tmp2 = q.y*q.w;
    m20 = 2.0 * (tmp1 - tmp2)*invs ;
    m02 = 2.0 * (tmp1 + tmp2)*invs ;
    tmp1 = q.y*q.z;
    tmp2 = q.x*q.w;
    m21 = 2.0 * (tmp1 + tmp2)*invs ;
    m12 = 2.0 * (tmp1 - tmp2)*invs ;      
}

Alternative Java code 

    xx      = X * X;
    xy      = X * Y;
    xz      = X * Z;
    xw      = X * W;

    yy      = Y * Y;
    yz      = Y * Z;
    yw      = Y * W;

    zz      = Z * Z;
    zw      = Z * W;

m00  = 1 - 2 * ( yy + zz );
m01  =     2 * ( xy - zw );
m02 =     2 * ( xz + yw );

m10  =     2 * ( xy + zw );
m11  = 1 - 2 * ( xx + zz );
m12  =     2 * ( yz - xw );

m20  =     2 * ( xz - yw );
m21  =     2 * ( yz + xw );
m22 = 1 - 2 * ( xx + yy );

m03  = m13 = m23 = m30 = m31 = m32 = 0;
m33 = 1;

Derivation of Equations

To transform point P2 to point P1 we use

P2=q * P1 * q' (see here for details)

we want to find the matrix [M] that will do the same transform.

P2 = [M] P1

So assume P1 = (0,x,y,z) then multiplying out gives:

q * P1 * q'= ( - qx*x -qy* y- qz*z + i ( qw*x + qy*z- qz*y) + j (qw*y - qx*z + qz*x) + k (qw*z + qx*y - qy*x ) ) * (qw - i qx - j qy - k qz)

= (- qx*x -qy* y- qz*z)*qw - ( qw*x + qy*z- qz*y)*-qx -(qw*y - qx*z + qz*x)*-qy- (qw*z + qx*y - qy*x )*-qz
+ i (( qw*x + qy*z- qz*y)*qw + (- qx*x -qy* y- qz*z)*-qx + (qw*y - qx*z + qz*x)*-qz- (qw*z + qx*y - qy*x )*-qy)
+ j ((- qx*x -qy* y- qz*z)*-qy - ( qw*x + qy*z- qz*y)*-qz+ (qw*y - qx*z + qz*x)*qw + (qw*z + qx*y - qy*x )*-qx)
+ k ((- qx*x -qy* y- qz*z)*-qz + ( qw*x + qy*z- qz*y)*-qy - (qw*y - qx*z + qz*x)*-qx + (qw*z + qx*y - qy*x )*qw)

= - qx*qw*x -qy*qw* y- qz*qw*z + qw*qx*x + qy*qx*z - qz*qx*y + qw* qy*y - qx* qy*z + qz* qy*x + qw*qz*z + qx*qz*y - qy*qz*x
+ i ( qw*qw*x + qy*qw*z- qz*qw*y + qx*qx*x +qy*qx* y+ qz*qx*z - qw*qz*y + qx*qz*z - qz*qz*x + qw*qy*z + qx*qy*y - qy*qy*x
+ j ( qx*qy*x +qy*qy* y+ qz*qy*z + qw*qz*x +qy*qz*z- qz*qz*y + qw*qw*y - qx*qw*z + qz*qw*x - qw*qx*z - qx*qx*y + qy*qx*x )
+ k (qx*qz*x +qy*qz* y+ qz*qz*z - qw*qy*x - qy*qy*z+ qz*qy*y + qw*qx*y - qx*qx*z + qz*qx*x + qw*qw*z + qx*qw*y - qy*qw*x )

grouping the x,y and z terms and puting them in a matrix gives:

qw*qw + qx*qx- qz*qz- qy*qy - qz*qw+qy*qx- qw*qz+ qx*qy qy*qw + qz*qx + qx*qz + qw*qy
qx*qy+ qw*qz+ qz*qw+ qy*qx qy*qy- qz*qz+ qw*qw - qx*qx qz*qy+qy*qz- qx*qw- qw*qx
qx*qz- qw*qy+ qz*qx- qy*qw qy*qz + qz*qy+ qw*qx+ qx*qw qz*qz- qy*qy- qx*qx+ qw*qw

since qw*qw + qx*qx+ qz*qz+ qy*qy = 1 this gives

1- 2*qz*qz- 2*qy*qy - 2* qz*qw+2*qy*qx 2*qy*qw +2* qz*qx
2*qx*qy+ 2*qw*qz 1 - 2*qz*qz - 2*qx*qx 2*qz*qy- 2*qx*qw
2*qx*qz- 2*qw*qy 2*qy*qz + 2*qw*qx 1- 2*qy*qy- 2*qx*qx

Rotation about a point other than origin

Quaternions and 3x3 matrices alone can only represent rotations about the origin. But if we include a 3D vector with the quaternion we can use this to represent the point about which we are rotating. Also if we use a 4x4 matrix then this can hold a translation (as explained here) and therefore can specify a rotation about a point.

The following code generates a 4x4 matrix from a quaternion and a vector. The derivation is given here.

void setRotate(sfquat q,sfvec3f centre) {
   double sqw = q.w*q.w;
   double sqx = q.x*q.x;
   double sqy = q.y*q.y;
   double sqz = q.z*q.z;
   m00 = sqx - sqy - sqz + sqw; // since sqw + sqx + sqy + sqz =1
   m11 = -sqx + sqy - sqz + sqw;
   m22 = -sqx - sqy + sqz + sqw;
   
   double tmp1 = q.x*q.y;
   double tmp2 = q.z*q.w;
   m01 = 2.0 * (tmp1 + tmp2);
   m10 = 2.0 * (tmp1 - tmp2);
   
   tmp1 = q.x*q.z;
   tmp2 = q.y*q.w;
   m02 = 2.0 * (tmp1 - tmp2);
   m20 = 2.0 * (tmp1 + tmp2);
   
   tmp1 = q1.y*q.z;
   tmp2 = q1.x*q.w;
   m12 = 2.0 * (tmp1 + tmp2);
   m21 = 2.0 * (tmp1 - tmp2);
   
	double a1,a2,a3;
	 if (centre == null) {
		a1=a2=a3=0;
     } else {
		a1 = centre.x;
		a2 = centre.y;
	    a3 = centre.z;
	}
	m03 = a1 - a1 * m00 - a2 * m01 - a3 * m02;
	m13 = a2 - a1 * m10 - a2 * m11 - a3 * m12;
	m23 = a3 - a1 * m20 - a2 * m21 - a3 * m22;
	m30 = m31 = m32 = 0.0;
	m33 = 1.0;
}

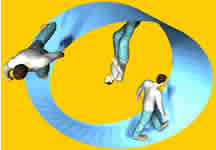
Example

we take the 90 degree rotation from this: to this:

As shown here the quaternion for this rotation is: (0.7071+ i 0.7071)

1- 2*qz*qz- 2*qy*qy - 2* qz*qw+2*qy*qx 2*qy*qw +2* qz*qx
2*qx*qy+ 2*qw*qz 1 - 2*qz*qz - 2*qx*qx 2*qz*qy- 2*qx*qw
2*qx*qz- 2*qw*qy 2*qy*qz + 2*qw*qx 1- 2*qy*qy- 2*qx*qx

So substituting this example gives:

1 0 0
0 1 - 2*0.5 = 0 - 2*0.5 = -1
0 2*0.5 =1 1- 2*0.5 =0

which is:

1 0 0
0 0 -1
0 1 0

So this gives the correct result shown here.

Angle Calculator and Further examples

I have put a java applet here which allows the values to be entered and the converted values shown along with a graphical representation of the orientation.

Also further examples in 90 degree steps here

metadata block
see also:
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover us uk de jp fr ca Matrix Computations

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.