Rotations can be represented by orthogonal matrices ( there is an equivalence with quaternion multiplication as described here)
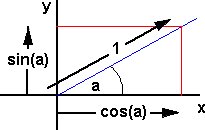
First rotation about z axis, assume a rotation of 'a' in an anticlockwise direction, this can be represented by a vector in the positive z direction (out of the page).
If we take the point (x=1,y=0) this will rotate to the point (x=cos(a),y=sin(a))
If we take the point (x=0,y=1) this will rotate to the point (x=-sin(a),y=cos(a))
3D rotations
For an alterative we to think about using a matrix to represent rotation see basis vectors here.
Rotation about the z axis
is given by the following matrix:
| Rotation about z axis is: Rz = |
|
For example if we choose an angle of +90 degrees we get
| 0 | -1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
the direction of rotation is given by the right hand rule 
where the thumb is in the +z direction (toward the viewer) and the fingers show
the positive direction of rotation so 
will be rotated to 
.
The conventions used are explained here and the relationship to other standards here.
Other 90 degrees steps are shown here.
Similarly with rotation about y axis:
| Rotation about y axis is: Ry = |
|
For example if we choose an angle of +90 degrees we get
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| -1 | 0 | 0 |
the direction of rotation is given by the right hand rule 
where the thumb is in the +y direction (up) and the fingers show the positive
direction of rotation so
will be rotated to 
.
And rotation about x axis:
| Rotation about x axis is: Rx = |
|
For example if we choose an angle of +90 degrees we get
| 1 | 0 | 0 |
| 0 | 0 | -1 |
| 0 | 1 | 0 |
the direction of rotation is given by the right hand rule 
where the thumb is in the +x direction (right) and the fingers show the positive
direction of rotation so
will be rotated to 
.
General rotation matrix:
| Rotation about a general axis is: |
|
This general rotation can be represented by a combination of the above rotations about Rz, Ry and Rx. As explained below the order of these rotations is important, there are different conventions for which order is assumed, as explained here.
Rotation matrices are orthogonal as explained here.
for Java and C++ code to implement these rotations click here
isRotationMatrix
This code checks that the input matrix is a pure rotation matrix and does not contain any scaling factor or reflection for example
/**
*This checks that the input is a pure rotation matrix 'm'.
* The condition for this is:
* R' * R = I
* and
* det(R) =1
*/
public boolean isRotationMatrix(matrix m) {
double epsilon = 0.01; // margin to allow for rounding errors
if (Math.abs(m[0][0]*m[0][1] + m[0][1]*m[1][1] + m[0][2]*m[1][2]) > epsilon) return false;
if (Math.abs(m[0][0]*m[2][0] + m[0][1]*m[2][1] + m[0][2]*m[2][2]) > epsilon) return false;
if (Math.abs(m[1][0]*m[2][0] + m[1][1]*m[2][1] + m[1][2]*m[2][2]) > epsilon) return false;
if (Math.abs(m[0][0]*m[0][0] + m[0][1]*m[0][1] + m[0][2]*m[0][2] - 1) > epsilon) return false;
if (Math.abs(m[1][0]*m[1][0] + m[1][1]*m[1][1] + m[1][2]*m[1][2] - 1) > epsilon) return false;
if (Math.abs(m[2][0]*m[2][0] + m[2][1]*m[2][1] + m[2][2]*m[2][2] - 1) > epsilon) return false;
return (Math.abs(det(m)-1) < epsilon);
// det is defined here:
// https://www.euclideanspace.com/maths/algebra/matrix/functions/determinant/threeD/
}
Successive Rotations
The order of Successive Rotations is significant, for example
- Rotate 90 degrees about x axis
- Rotate 90 degrees about y axis
- Rotate -90 degrees about x axis
This gives 90 degree rotation about Z axis,
whereas
- Rotate 90 degrees about x axis
- Rotate -90 degrees about x axis
- Rotate 90 degrees about y axis
This gives 90 degree rotation about y axis (first 2 lines cancel out).
Successive rotations can be calculated by multiplying together the matrices representing the individual rotations. In the same way that the order of rotations are important, the order of matrix multiplication is important.
So with matrix algebra different rules apply than in the algebra of numbers.
In the first example the 3 rotations would be represented by:
|
× |
|
× |
|
= |
|
in the second case the rotations are represented by:
|
× |
|
× |
|
= |
|
Axis Angle rotation
Any set of successive rotations can be replaced by a single equivalent rotation:
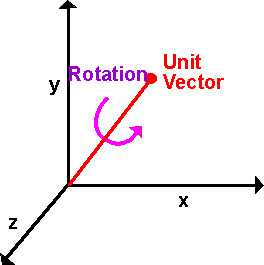
The matrix for this rotation is given by:
