On the HoTT page we looked at Voevodsky's 'univalence axiom' (A=B)
(AB). (identity is equivalent to equivalence).
On this page we try to investigate examples of this equivalence which is like isomorphism.
One way to interpret this might be that isomorphism is like equality in multiple ways.
Equality of Bool
| For instance, in the Boolean example, if we set: 0 = false 1 = true then the sets are equal. |
 |
| Alternatively if we set: 0 = true 1 = false then the sets are equal in a different way. |
 |
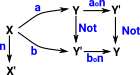
There is a higher order morphism (a natural transformation) called 'not' between these 'equalities. |
 |
Here is the naturality square: This square needs to commute. |
 |
Equality of Finite Set
For the next example lets go from a 2 element set to a 3 element set. If we have a set with 3 elements there are 6 ways that it can be equal to another such set (the number of permutations of 3 elements = !3 = 6. There is a natural transformation between each of these 6 'equalities' and every other one (I've only shown some of them, in blue, on the diagram. |
Lets look at equality between two 3-element sets, say, data primary = R | G | B and data secondary C | M | Y |
Each of these natural transformations has an inverse going in the opposite direction.
We can see how this has the structure of a groupoid. For instance, every natural transformation has an inverse.
More about groupoids on the page here
Induction of Set Permutations
If we have a set with 'n' elements and there are 'x' permutations between two such sets. If we then add an element so we have 'n+1' elements then the number of permutations is now 'x*(n+1)' . S the number of permutations is n! that in nfactorial. |
 |
Higher Order Equality
What happens if we have a two element set whose elements are sets? Can we relate the morphisms between the inner sets to morphisms between the outer sets? |
 |
| Iv'e tried to draw a hierachy of naturality squares. |  |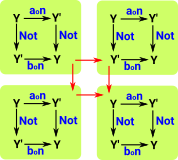
